AP Calculus AB 2015 Question 5 and Answers
Related Topics:
More videos, activities and worksheets that are suitable for Calculus
Questions and Worked Solutions for AP Calculus AB 2015.
(a) Find all x-coordinates at which f has a relative maximum. Give a reason for your answer.
(b) On what open intervals contained in -3 < x < 4 is the graph of f both concave down and decreasing?
Give a reason for your answer.
(c) Find the x-coordinates of all points of inflection for the graph of f. Give a reason for your answer.
(d) Given that f(1) = 3, write an expression for f(x) that involves an integral. Find f(4) and f(-2).
More videos, activities and worksheets that are suitable for Calculus
Questions and Worked Solutions for AP Calculus AB 2015.
AP Calculus AB 2015 Free Response Questions - Complete Paper (pdf)
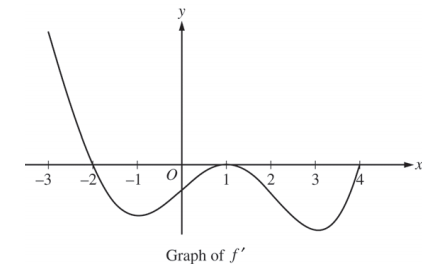
(a) Find all x-coordinates at which f has a relative maximum. Give a reason for your answer.
(b) On what open intervals contained in -3 < x < 4 is the graph of f both concave down and decreasing?
Give a reason for your answer.
(c) Find the x-coordinates of all points of inflection for the graph of f. Give a reason for your answer.
(d) Given that f(1) = 3, write an expression for f(x) that involves an integral. Find f(4) and f(-2).
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.