AP Calculus AB and BC 2015 Question 1 and Answers
Related Topics:
More videos, activities and worksheets that are suitable for Calculus
Questions and Worked Solutions for AP Calculus AB 2015.
1. The rate at which rainwater flows into a drainpipe is modeled by the function R, where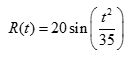
cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain
out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for
0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0.
(a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
(b) Is the amount of water in the pipe increasing or decreasing at time t 3 hours? Give a reason for your answer.
(c) At what time t, 0 ≤ t ≤ 8, is the amount of water in the pipe at a minimum? Justify your answer.
(d) The pipe can hold 50 cubic feet of water before overflowing. For t > 8, water continues to flow into and out of the pipe at the given rates until the pipe begins to overflow. Write, but do not solve, an equation involving one or more integrals that gives the time w when the pipe will begin to overflow.
More videos, activities and worksheets that are suitable for Calculus
Questions and Worked Solutions for AP Calculus AB 2015.
AP Calculus AB 2015 Free Response Questions - Complete Paper (pdf)
AP Calculus BC 2015 Free Response Questions - Complete Paper (pdf)
1. The rate at which rainwater flows into a drainpipe is modeled by the function R, where
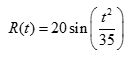cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain
out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for
0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0.
(a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?(b) Is the amount of water in the pipe increasing or decreasing at time t 3 hours? Give a reason for your answer.
(c) At what time t, 0 ≤ t ≤ 8, is the amount of water in the pipe at a minimum? Justify your answer.
(d) The pipe can hold 50 cubic feet of water before overflowing. For t > 8, water continues to flow into and out of the pipe at the given rates until the pipe begins to overflow. Write, but do not solve, an equation involving one or more integrals that gives the time w when the pipe will begin to overflow.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.