

AP Calculus AB and BC 2014 Question 4 and Answers
Related Topics:
More videos, activities and worksheets that are suitable for Calculus
Questions and Worked Solutions for AP Calculus AB and BC 2014.
(a) Find the average acceleration of train A over the interval 2 ≤ t ≤ 8.
(b) Do the data in the table support the conclusion that train A’s velocity is -100 meters per minute at some time t with 5 < t < 8 ? Give a reason for your answer.
(c) At time t = 2, train A’s position is 300 meters east of the Origin Station, and the train is moving to the east. Write an expression involving an integral that gives the position of train A, in meters from the Origin Station, at time t = 12. Use a trapezoidal sum with three subintervals indicated by the table to approximate the position of the train at time t = 12.
(d) A second train, train B, travels north from the Origin Station. At time t the velocity of train B is given by VB(t) = -5t2 + 60t + 25 and at time t = 2 the train is 400 meters north of the station. Find the rate, in meters per minute, at which the distance between train A and train B is changing at time t = 2



More videos, activities and worksheets that are suitable for Calculus
Questions and Worked Solutions for AP Calculus AB and BC 2014.
AP Calculus AB 2014 Free Response Questions - Complete Paper (pdf)
AP Calculus BC 2014 Free Response Questions - Complete Paper (pdf)
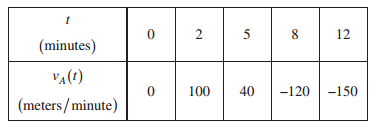
(a) Find the average acceleration of train A over the interval 2 ≤ t ≤ 8.
(b) Do the data in the table support the conclusion that train A’s velocity is -100 meters per minute at some time t with 5 < t < 8 ? Give a reason for your answer.
(c) At time t = 2, train A’s position is 300 meters east of the Origin Station, and the train is moving to the east. Write an expression involving an integral that gives the position of train A, in meters from the Origin Station, at time t = 12. Use a trapezoidal sum with three subintervals indicated by the table to approximate the position of the train at time t = 12.
(d) A second train, train B, travels north from the Origin Station. At time t the velocity of train B is given by VB(t) = -5t2 + 60t + 25 and at time t = 2 the train is 400 meters north of the station. Find the rate, in meters per minute, at which the distance between train A and train B is changing at time t = 2
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.