Illustrative Mathematics Grade 7, Unit 7, Lesson 1: Relationships of Angles

Related Pages
Illustrative Math
Grade 7

Lesson 1: Relationships of Angles

Let’s examine some special angles.

Illustrative Math Unit 7.7, Lesson 1 (printable worksheets)

Lesson 1 Summary

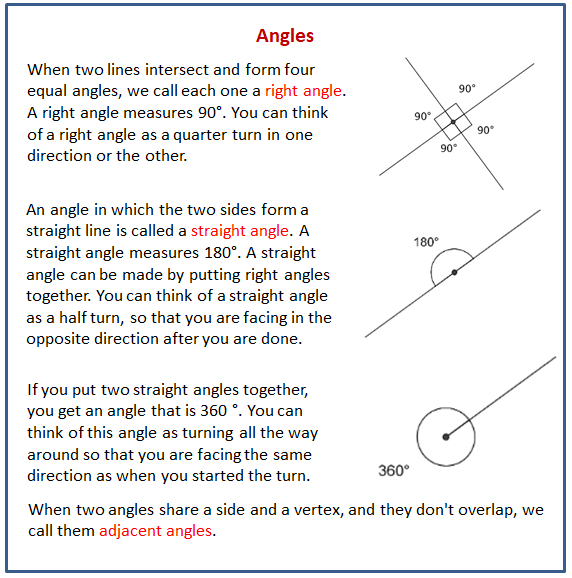
The following diagram shows some special angles: 90°, 180°, 360°, or adjacent angles.

Lesson 1.1 Visualizing Angles

Use the applet to answer the questions.
Which angle is bigger, a or b?
Identify an obtuse angle in the diagram.
Open Applet

• See Video for Whole Lesson

Lesson 1.2 Pattern Block Angles

1. Look at the different pattern blocks inside the applet. Each block contains either 1 or 2 angles with different degree measures. Which blocks have only 1 unique angle? Which have 2?
2. If you place three copies of the hexagon together so that one vertex from each hexagon touches the same point, as shown, they fit together without any gaps or overlaps. Use this to figure out the degree measure of the angle inside the hexagon pattern block.
3. Figure out the degree measure of all of the other angles inside the pattern blocks. (Hint: turn on the grid to help align the pieces.) Open Applet

Are you ready for more?

We saw that it is possible to fit three copies of a regular hexagon snugly around a point.
Each interior angle of a regular pentagon measures 108°. Is it possible to fit copies of a regular pentagon snugly around a point? If yes, how many copies does it take? If not, why not?

• Show Answer

  Each interior angle of a regular hexagon measures 120°. Three copies of a regular hexagon snugly around a point because 360 ÷ 120 = 3.
  Each interior angle of a regular pentagon measures 108°. 360 ÷ 108 = 3 1/3, which is not a whole number. This means that it would not be possible to fit the copies of a regular pentagon snugly around a point.

Lesson 1.3 More Pattern Block Angles

1. Use pattern blocks to determine the measure of each of these angles.
2. If an angle has a measure of 180° then the two legs form a straight line. An angle that forms a straight line is called a straight angle. Find as many different combinations of pattern blocks as you can that make a straight angle.
   Use the applet if you choose. (Hint: turn on the grid to help align the pieces.)
   Open Applet

Lesson 1.4 Measuring Like This or That

Tyler and Priya were both measuring angle TUS.
Priya thinks the angle measures 40 degrees. Tyler thinks the angle measures 140 degrees. Do you agree with either of them? Explain your reasoning.

Lesson 1 Practice Problems

1. Here are questions about two types of angles.
   Draw a right angle. How do you know it’s a right angle? What is its measure in degrees?
   Draw a straight angle. How do you know it’s a straight angle? What is its measure in degrees?
   
2. An equilateral triangle’s angles each have a measure of 60 degrees.
   a. Can you put copies of an equilateral triangle together to form a straight angle? Explain or show your reasoning.
   b. Can you put copies of an equilateral triangle together to form a right angle? Explain or show your reasoning.
   
3. Here is a square and some regular octagons.
   In this pattern, all of the angles inside the octagons have the same measure. The shape in the center is a square. Find the measure of one of the angles inside one of the octagons.
4. The height of the water in a tank decreases by 3.5 cm each day. When the tank is full, the water is 10 m deep. The water tank needs to be refilled when the water height drops below 4 m. Write a question that could be answered by solving the equation 10 - 0.035d = 4.
   Is 100 a solution of 10 - 0.035d > 4? Write a question that solving this problem could answer.
5. Use the distributive property to write an expression that is equivalent to each given expression.
6. Lin’s puppy is gaining weight at a rate of 0.125 pounds per day. Describe the weight gain in days per pound.

The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.