Circles and Angles (Grade 4)

Videos, examples, solutions, and lessons to help Grade 4 students learn to recognize angles as geometric shapes that are formed wherever two rays share a common endpoint, and understand concepts of angle measurement.

A. An angle is measured with reference to a circle with its center at the common endpoint of the rays, by considering the fraction of the circular arc between the points where the two rays intersect the circle. An angle that turns through 1/360 of a circle is called a “one-degree angle,” and can be used to measure angles.
B. An angle that turns through n one-degree angles is said to have an angle measure of n degrees.

Common Core: 4.MD.5

Suggested Learning Targets

• I can identify the parts of an angle and define what an angle is.
• I can explain that an angle is measured in degrees

Angles in relation to Circles- 4.MD.5
In this video, students will learn about angles measured in degrees and their relationship to a circle. This video relates to Common Core Standard 4.MD.5. It reviews types of fractional turns and how to find an angle measure using a fraction of a circle

The following activities are obtained from the Howard County Public School System.

Activity 1:
A circle measures 360°.  If the circle were divided into 4 equal parts, what would be the angle measurement of each part?  Explain how you know.

Activity 2:
Matthew and Nick were investigating angles and circles, drawing circles and creating angles inside of their circles.
Matthew drew a small circle and divided it into six equal sections.  He measured the angles of each section and found that they were all 60º.
Nick decided to draw a circle that was larger than Matthew’s circle.  He divided his circle into six equal sections and measured the angles of each section.  He expected them to be larger than 60º, but they all measured 60º.

The resource sheet Circles and Angles shows the work that Matthew and Nick did.

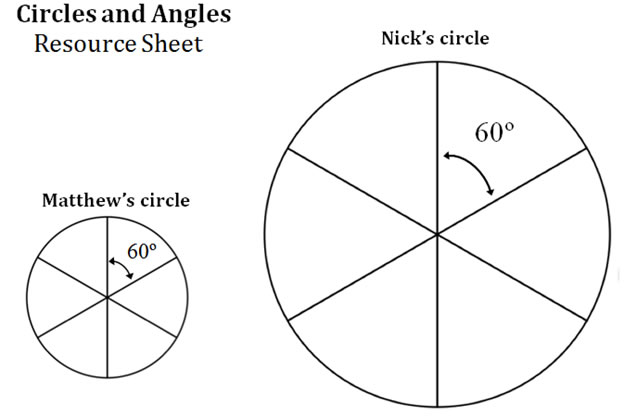
Why might Nick have thought the sections of his circle would have a larger angle measurement than the sections in Matthew’s circle?

Why do the sections in Nick’s circle and the sections in Matthew’s circle have the same angle measurement?

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.