Triangle Sum Theorem

What is the Triangle Sum Theorem?

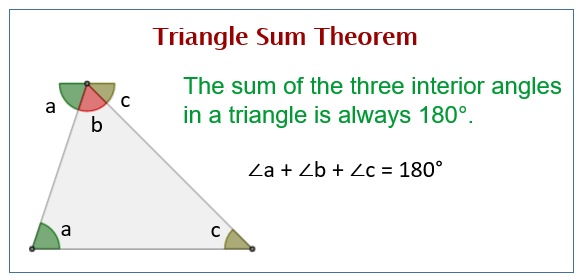
The Triangle Sum Theorem states that the sum of the interior angles of a triangle equal 180°.

The following diagram shows an example of the Triangle Sum Theorem. Scroll down the page for examples and solutions.

 

Geometry Worksheets
Practice your skills with the following Geometry worksheets:
Printable & Online Geometry Worksheets

If we have a triangle with interior angles labeled as \(A\), \(B\), and \(C\), then the Triangle Sum Theorem can be expressed as the equation:

\(m\angle A+ m\angle B + m\angle C\) = 180°
Where \(m\angle\) denotes the measure of the angle in degrees.

Key Points about the Triangle Sum Theorem:

• Universality: This theorem applies to all types of triangles, regardless of their shape or size. Whether the triangle is acute, obtuse, or right, the sum of its interior angles will always be 180°.
• Finding Missing Angles: The most common application of the Triangle Sum Theorem is to find the measure of a missing angle in a triangle when the measures of the other two angles are known.
• Proofs: There are several ways to prove the Triangle Sum Theorem. One common method involves drawing a line parallel to one side of the triangle through the opposite vertex and using the properties of alternate interior angles and angles on a straight line.
• Euclidean Geometry: The Triangle Sum Theorem holds true in Euclidean geometry (the geometry of flat surfaces). In non-Euclidean geometries, such as spherical or hyperbolic geometry, the sum of the interior angles of a triangle can be different from 180°.

Triangle Angle Sum
The sum of the three angles in any triangle sum to 180 degrees. The importance of this fact in Geometry cannot be emphasized enough. The triangle angle sum theorem is used in almost every missing angle problem, in the exterior angle theorem, and in the polygon angle sum formula.
This video, discusses the sum of the interior angles of a triangle always equals 180 degrees. There are 4 example problems from easy, medium, medium-hard, and hard.

• Show Video

Angles of a Triangle - Triangle Sum Theorem with Algebra
Students learn the triangle sum theorem, which states that the sum of the measures of the angles of a triangle is 180 degrees. Students are then asked to solve problems related to the triangle sum theorem using Algebra.

• Show Step-by-step Solutions

Angle Sum of a Triangle

• Show Step-by-step Solutions

Geometry Word Problems - Angles of a Triangle
Example:
The measures of the angles of a triangle are in the ratio 2:5:8. Find the measure of each angle.

• Show Step-by-step Solutions

Examples of Using the Triangle Sum Theorem:
Example: Finding a Missing Angle
In a triangle, two angles measure 60° and 80°. Find the measure of the third angle.
Let the measures of the three angles be \(A = 60^\circ\), \(B = 80^\circ\), and \(C = x\).
Using the Triangle Sum Theorem:
60° + 80° + \(x\) = 180
140° + \(x\) = 180
\(x\) = 180° − 140°
\(x\) = 40°
So, the measure of the third angle is (40°).

Example: Using Algebra to Find Angles
The measures of the three angles of a triangle are y°, (y + 20)°, and (2y + 40)°. Find the value of y and the measure of each angle.
Using the Triangle Sum Theorem:
y + (y+20) + (2y+40) = 180
4y + 60 = 180
4y = 180 − 60
4y = 120
y = 120/4
y = 30

Now, substitute the value of y to find the measure of each angle:
First angle: y = 30°
Second angle: (30 + 20)° = 50°
Third angle: 2(30) + 40° = 100°
Check: 30° + 50° + 100° = 180°

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.