Angles of Elevation and Depression: Examples

Angles of Elevation and Depression

Angles of elevation and depression are used in trigonometry to measure angles relative to the horizontal line of sight.

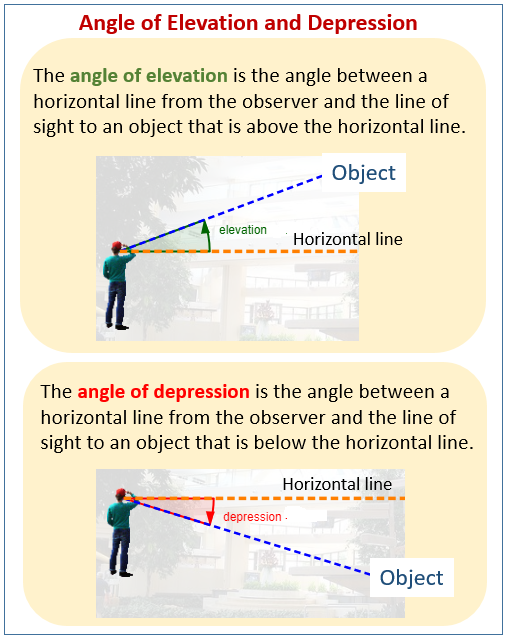
The following figures show some examples of angle of elevation and angle of depression. Scroll down the page for more examples and solutions on solving problems with angle of elevation or angle of depression.

 

Trigonometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Trigonometry Worksheets

The angle of elevation is the angle formed when an observer looks up at an object.
Observer’s Position: Below the object.
Line of Sight: Goes upwards from the observer’s eye to the object.
Horizontal Line: A theoretical line extending straight out from the observer’s eye level, parallel to the ground.
The Angle: The angle is formed above the horizontal line.

The angle of depression is the angle formed when an observer looks down at an object.
Observer’s Position: Above the object.
Line of Sight: Goes downwards from the observer’s eye to the object.
Horizontal Line: A theoretical line extending straight out from the observer’s eye level, parallel to the ground.
The Angle: The angle is formed below the horizontal line.

Videos

Angles of Depression and Elevation
Learn about angles of depression and elevation.

• Show Step-by-step Solutions

Find the height of a dam using angle of elevation and the height of a helicopter using the concept of angle of depression
Examples:

1. From a point 340 m from the base of Hoover Dam, the angle of elevation to the top of the dam is 33 degrees. Find the height of the dam to the nearest meter.
2. A helicopter pilot sights a life raft. The angle of depression is 28 degrees and the helicopter’s altitude is 2.5 km
   (a) Draw a figure to represent the situation.
   (b) What is the horizontal distance from the helicopter to the raft?
   (c) If the helicopter flies at a constant speed of 200 km/hr, how long will it be before it is directly above the raft? Assume that the altitude of the helicopter doesn’t change.

• Show Step-by-step Solutions

Trigonometry Word Problems
Students solve word problems using sine, cosine, and tangent. The terms angle of elevation and angle of depression are also introduced in this lesson.
Example:
Neil sees a rocket at an angle of elevation of 11°. If Neil is located 5 miles from the rocket’s launchpad, how high is the rocket? Round your answer to the nearest hundredth.

• Show Step-by-step Solutions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.