Angle Bisector Theorem
Examples, solutions, videos, worksheets, games and activities to help Geometry students learn about the triangle angle bisector theorem.
What is the Triangle Angle Bisector Theorem?
If a ray bisects an angle of a triangle, then it divides the opposite side of the triangle into segments that are proportional to the other two sides.
The following figure gives an example of the Angle Bisector Theorem. Scroll down the page for more examples and solutions.
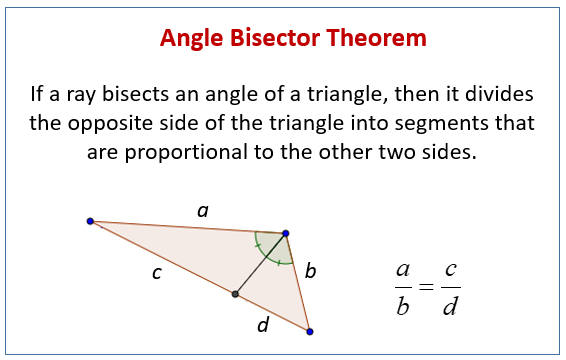
Triangle Angle Bisector Theorem
Using the Triangle-Angle-Bisector Theorem to solve a problem.
Angle Bisector Theorem Proof
Proof with Algebra - Angle Bisector Theorem Review
This math problem requires a two column proof to justify finding the value of x to satisfy the given statement.
Triangle Angle Bisector Theorem - Math Help
Students learn the following theorems related to similar triangles.
If a line is parallel to a side of a triangle, and it intersects the other two sides of the triangle, then it divides these sides proportionally (Triangle Proportionality Theorem).
If three parallel lines intersect two transversals, then they divide the transversals proportionally (Corollary of the Triangle Proportionality Theorem).
If a ray bisects an angle of a triangle, then it divides the opposite side of the triangle into segments that are proportional to the other two sides (Triangle Angle-Bisector Theorem).
Students are then asked to solve problems related to these theorems using Algebra.
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.