Altitude of a Triangle
Examples, solutions, and videos that will help GMAT students review some questions on the altitude of a triangle.
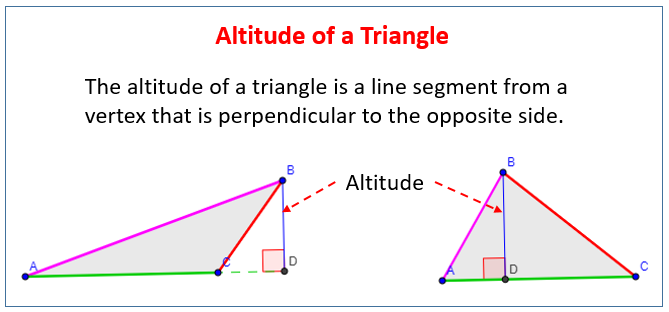
The following diagrams show the altitude of an acute triangle and an obtuse triangle. Scroll down the page for more examples and solutions.
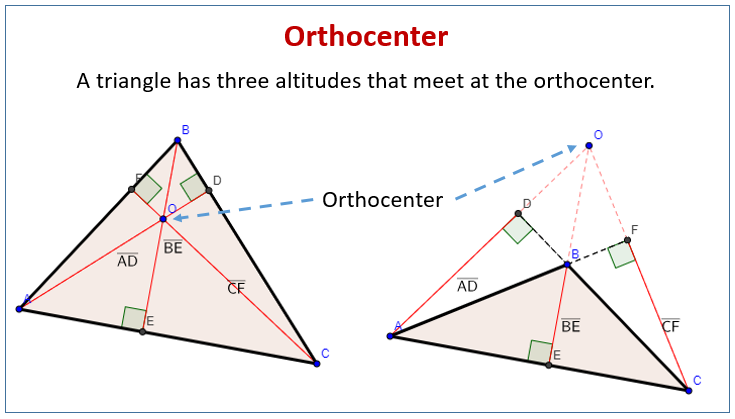
The following diagrams show the orthocenter of an acute triangle and an obtuse triangle. Scroll down the page for more examples and solutions.
What is the altitude of a triangle?
The altitude of a triangle is a line segment from a vertex that is perpendicular to the opposite side. A triangle has three altitudes. The point of concurrency is called the orthocenter.
The orthocenter can be inside, on, or outside the triangle based upon the type of triangle.
The Altitudes of a Triangle
This video defines an altitude and orthocenter of a triangle.
Constructing an Altitude of a Triangle
Altitude of a Triangle - Geometry Help
Students learn the definition of an altitude of a triangle,
How to Find the Altitude of a Right Triangle?
Isosceles Triangle Properties
In isosceles (and equilateral) triangles, a segment drawn from the vertex angle to the opposite side is the altitude, angle bisector and median. Isosceles triangle properties are used in many proofs and problems where the student must realize that, for example, an altitude is also a median or an angle bisector to find a missing side or angle.
Theorem: In an isosceles triangle ABC the median, bisector and altitude drawn from the angle made by the equal sides fall along the same line.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.