Algebra I Common Core Regents Exam - June 2017

Algebra I Common Core Regents New York State Exam - June 2017

The following are questions from the past paper Regents High School Algebra I June 2017 Exam (pdf). Scroll down the page for the step by step solutions.

Algebra 1 - June 2017 Regents - Questions and solutions 1 - 12

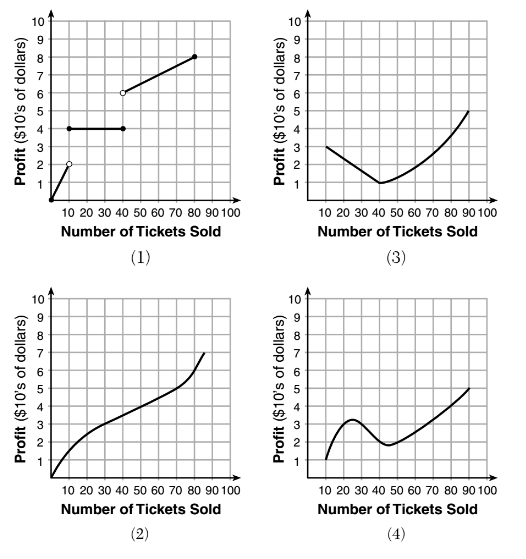
1. To keep track of his profi ts, the owner of a carnival booth decided computations. to model his ticket sales on a graph. He found that his profits only declined when he sold between 10 and 40 tickets. Which graph could represent his profits?
   
   
2. The formula for the surface area of a right rectangular prism is computations. A = 2lw + 2hw + 2lh, where l, w, and h represent the length, width, and height, respectively. Which term of this formula is not dependent on the height?
   
3. Which graph represents y = √(x - 2)?
   
4. A student plotted the data from a sleep study as shown in the graph below. The student used the equation of the line y = -0.09x + 9.24 to model the data. What does the rate of change represent in terms of these data?
   
5. Lynn, Jude, and Anne were given the function f(x) = -2x² + 32, and they were asked to find f(3). Lynn’s answer was 14, Jude’s answer was 4, and Anne’s answer was ±4. Who is correct?
   
6. Which expression is equivalent to 16x⁴ - 64?
   
7. Vinny collects population data, P(h), about a specific strain of bacteria over time in hours, h, as shown in the graph below.
   
8. What is the solution to the system of equations below?
   y = 2x + 8
   3(-2x + y) = 12
   
9. A mapping is shown in the diagram below.
   
10. Which polynomial function has zeros at -3, 0, and 4?
    
11. Jordan works for a landscape company during his summer vacation. He is paid $12 per hour for mowing lawns and $14 per hour for planting gardens. He can work a maximum of 40 hours per week, and would like to earn at least $250 this week. If m represents the number of hours mowing lawns and g represents the number of hours planting gardens, which system of inequalities could be used to represent the given conditions?
    
12. Anne invested $1000 in an account with a 1.3% annual interest rate. She made no deposits or withdrawals on the account for 2 years. If interest was compounded annually, which equation represents the balance in the account after the 2 years?

• Show Step-by-step Solutions

Algebra 1 - June 2017 Regents - Questions and solutions 13 - 24

13. Which value would be a solution for x in the inequality 47 - 4x < 7?
    
14. Bella recorded data and used her graphing calculator to find the equation for the line of best fit. She then used the correlation coefficient to determine the strength of the linear fit.
    Which correlation coefficient represents the strongest linear relationship?
    
15. The heights, in inches, of 12 students are listed below.
    61, 67, 72, 62, 65, 59, 60, 79, 60, 61, 64, 63
    Which statement best describes the spread of these data?
    
16. The graph of a quadratic function is shown below.
    
17. Which statement is true about the quadratic functions g(x), shown in the table below, and f(x) = (x - 3)² + 2?
    
18. Given the function f(n) defined by the following:
    f(1) = 2
    f(n) = -5f(n - 1) + 2
    
19. An equation is given below.
    4(x 7) 0.3(x 2) 2.11
    
20. A construction worker needs to move 120 ft³ of dirt by using a wheelbarrow. One wheelbarrow load holds 8 ft³ of dirt and each load takes him 10 minutes to complete. One correct way to figure out the number of hours he would need to complete this job is
    
21. One characteristic of all linear functions is that they change by
    
22. What are the solutions to the equation x² - 8x = 10?
    
23. The formula for blood fl ow rate is given by F = (p₁ - p₂)/r, where F is the flow rate, p₁ the initial pressure, p₂ the final pressure, and r the resistance created by blood vessel size. Which formula can not be derived from the given formula?
    
24. Morgan throws a ball up into the air. The height of the ball above the ground, in feet, is modeled by the function h(t) = 16t² + 24t, where t represents the time, in seconds, since the ball was thrown.
    What is the appropriate domain for this situation?

• Show Step-by-step Solutions

Algebra 1 - June 2017 Regents - Questions and solutions 25 - 37

25. Express in simplest form: (3x² + 4x - 8) - (-2x² + 4x + 2)
    
26. Graph the function f(x)= -x² - 6x on the set of axes below.
    
27. State whether 7 - √2 is rational or irrational. Explain your answer.
    
28. The value, v(t), of a car depreciates according to the function v(t) = P(.85)^t, where P is the purchase price of the car and t is the time, in years, since the car was purchased. State the percent that the value of the car decreases by each year. Justify your answer.
    
29. A survey of 100 students was taken. It was found that 60 students watched sports, and 34 of these students did not like pop music. Of the students who did not watch sports, 70% liked pop music. Complete the two-way frequency table.
    
30. Graph the inequality y + 4 < -2(x - 4) on the set of axes below.
    
31. If f(x) = x² and g(x)= x, determine the value(s) of x that satisfy the equation f(x) = g(x).
    
32. Describe the effect that each transformation below has on the function f(x) = |x|, where a > 0.
    g(x) = |x - a|
    h(x) = |x| - a
    
33. The function r(x) is defined by the expression x² + 3x - 18. Use factoring to determine the zeros of r(x).
    Explain what the zeros represent on the graph of r(x).
    
34. The graph below models Craig’s trip to visit his friend in another state. In the course of his travels, he encountered both highway and city driving.
    Based on the graph, during which interval did Craig most likely drive in the city? Explain your reasoning.
    Explain what might have happened in the interval between B and C.
    Determine Craig’s average speed, to the nearest tenth of a mile per hour, for his entire trip.
    
35. Given:
    g(x) = 2x² + 3x + 10
    k(x) = 2x + 16
    Solve the equation g(x) 2k(x) algebraically for x, to the nearest tenth.
    Explain why you chose the method you used to solve this quadratic equation.
    
36. Michael has $10 in his savings account. Option 1 will add $100 to his account each week.
    Option 2 will double the amount in his account at the end of each week.
    Write a function in terms of x to model each option of saving.
    Michael wants to have at least $700 in his account at the end of 7 weeks to buy a mountain bike.
    Determine which option(s) will enable him to reach his goal. Justify your answer.
    
37. Central High School had fi ve members on their swim team in 2010. Over the next several years, the team increased by an average of 10 members per year. The same school had 35 members in their chorus in 2010. The chorus saw an increase of 5 members per year.
    Write a system of equations to model this situation, where x represents the number of years since 2010.
    Graph this system of equations on the set of axes below.
    Explain in detail what each coordinate of the point of intersection of these equations means in the context of this problem.

• Show Step-by-step Solutions

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.