Adding Rational Expressions
In these lessons, we will learn how to add rational expressions with the same denominator and how to add rational expressions with different denominators.
Related Pages
More Algebra Lessons
Algebra Worksheets
Algebra Games
A rational expression is a fraction in which either the numerator, or the denominator, or both the numerator and the denominator are algebraic expressions. For example, 
and 
are rational expressions.
Adding Rational Expressions with Same Denominators
When the denominators of two algebraic fractions are the same, we can add the numerators and then simplify when possible.
Example:
Simplify the following rational expression
Solution:
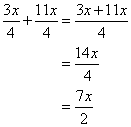
How to add rational expressions that have a common denominator, and how to simplify if it is possible to cancel?
How to add or subtract rational expressions with same denominators?
Adding Rational Expressions with Different Denominators
When the denominators of two algebraic fractions are different, we need to find the LCM of the denominators (also called the LCD) before we add or subtract the fractions.
Here are the steps you need to follow:
Step 1: Find the LCD
Step 2: Express each fraction with the LCD as the denominator.
Step 3: Add the numerators and simplify when possible. Now we apply the above 3 steps in the following examples.
Example:
Express the following as fractions with a single denominator:
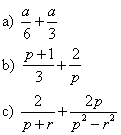
Solution:
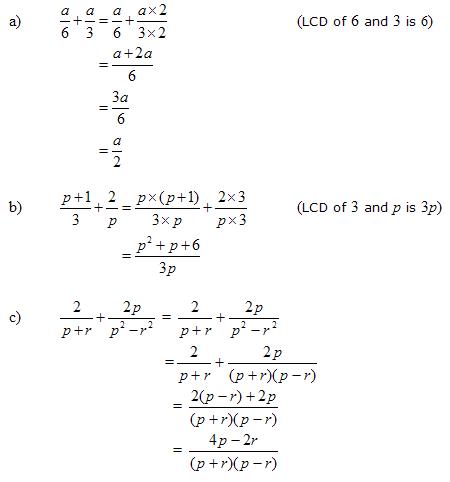
Add and Subtract Rational Expressions - Unlike Denominators
How to add and subtract rational expressions when the denominators are different?
How to add rational expressions with different denominators?
How to add rational expressions with different monomial denominators?
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.