Adding Fractions (like or unlike denominators)

Adding Fractions

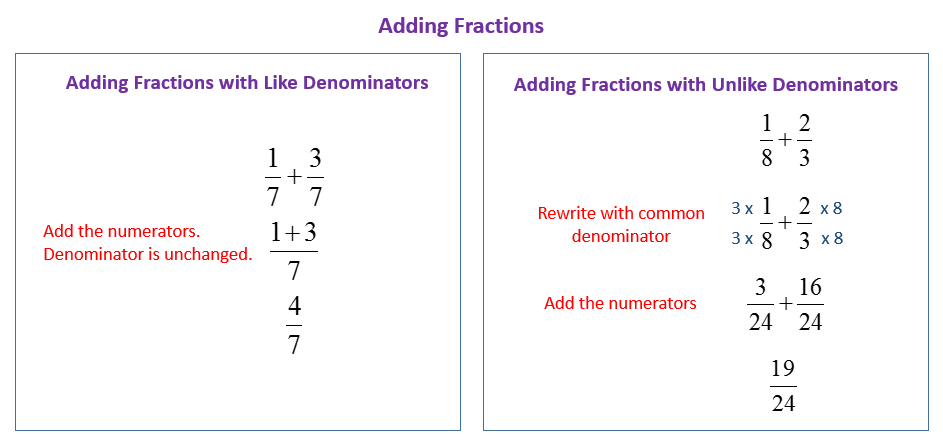
The method you use for adding fractions depends on whether the fractions have the same denominator or different denominators.

The following examples shows how to add fractions with like denominators and unlike denominators. Scroll down the page for more examples and solutions.

 

Fraction Worksheets
Practice with the following worksheets.
Printable & Online Fractions Worksheets

Adding Fractions with Common or Like Denominators

When we add fractions that have the same, or common denominators, we add only the numerators. The denominators stay the same.

Example

 

• Show Video

Adding Fractions With Uncommon or Unlike Denominators

To add fractions with uncommon denominators, we need to change the fractions to equivalent fractions with common denominators before we find the sum.

First, we would need to find the least common denominator (LCD), which is the LCM of the denominators.

Next, we write equivalent fractions using the least common denominator. Then, we proceed to add as before.

Example:

Evaluate

Solution:

Step 1: Find the LCD or LCM of 2 and 5

Multiples of 2: 2, 4, 6, 8, 10, 12

Multiples of 5: 5, 10, 15

The LCD or the Least Common Multiple of 2 and 5 is 10

Step 2: Write both fractions and as equivalent fractions with a common denominator of 10.

 

Step 3: Add the 2 equivalent fractions.

The following video shows more examples of adding fractions with uncommon or unlike denominators.

• Show Video

Check out this lesson on types of fractions:
Types of Fractions
Check out this lesson on equivalent fractions:
Equivalent Fractions
Check out this lesson on how to convert between mixed numbers and improper fractions:
Mixed Numbers & Improper Fractions
Check out this lesson on how to convert between fractions and decimals:
Fractions & Decimals

Check out these lessons on adding, subtracting, multiplying, and dividing fractions:
Adding Fractions
Subtracting Fractions
Multiplying Fractions
Dividing Fractions

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.