Acids, Bases, Salts
Related Topics:
More Lessons for IGCSE Chemistry
Math Worksheets
A series of free IGCSE Chemistry Lessons (Cambridge IGCSE Chemistry).
What is an acid? Acid and alkali solutions, Metal oxides and non-metal oxides, Acid reactions in everyday life, Alkalis and bases, Characteristic reactions of acids, Acids and alkalis in chemical analysis, Salts, Preparing soluble salts, Preparing insoluble salts, Strong and weak acids and alkalis.
The following table shows the neutralisation equations when acid reacts with metal, base, metal oxide, metal carbonate, ammonia, and when base reacts with ammonium salt, non-metal oxide. Scroll down the page for examples and explanations.
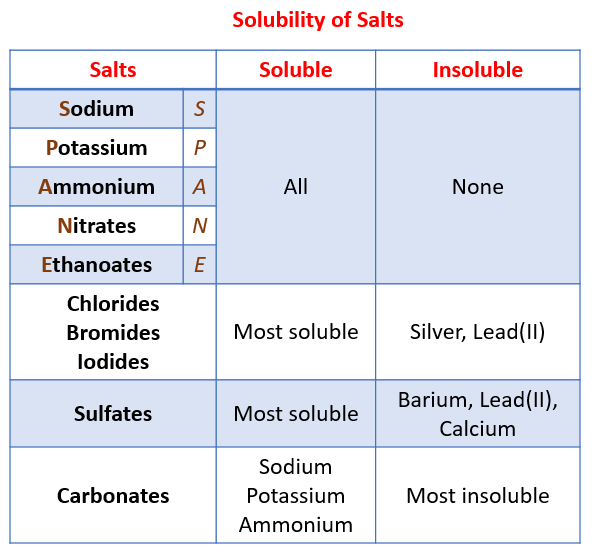
A salt is an ionic compound that can be formed by the neutralization reaction of an acid and a base. The following table shows the patterns for the solubility of salts. To help you remember, think of SPANE for soluble salts: Sodium, Potassium, Ammonium, Nitrates and Ethanoates. Scroll down the page for examples and solutions.
Weak and Strong Acids
Weak and Strong Bases
Acids and Bases: Indicators and pH
pH and strengths of Acids and Alkalis
Concentration of Acids and Alkalis
Differences between alkali and base
Characteristics of acids and alkali
Properties and uses of acids, bases and alkalis
Acidification of agricultural soils
Reaction of acids with bases and alkalis: neutralisation
The reaction of acids with carbonates
Tests for metal ions in salts using alkalis
How are acids and alkalis made?
Solubility of Salts
Making Soluble Salts: Acid plus solid metal, base or carbonate
Preparation of a Soluble Salt by Titration
How to produce salt by reacting acid with a metal oxide?
How to produce salt by reacting acid with a carbonate?
Solubility of Hydroxides
Aluminium and Zinc Hydroxides are amphoteric
Acids, Bases and Salts
The nature of acids, alkalis, bases and salts.
What are the different acid reactions which are used to make soluble salts, and the precipitation reactions which are used to make insoluble salts?
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.