3-D Objects - Grade 3
Related Topics:
More Grade 3 Math Topics
Videos, worksheets, games and activities to help Grade 3 students learn to describe 3-D objects according to the shape of the faces and the number of edges and vertices.
In these free math lessons, we will learn 3-D objects such as pyramids, prisms, cylinders, cones and spheres and their nets.
The following diagrams show some 3D shapes: cubes, prisms, pyramids, cylinders, cones and spheres. Scroll down the page for more examples and explanations.
-
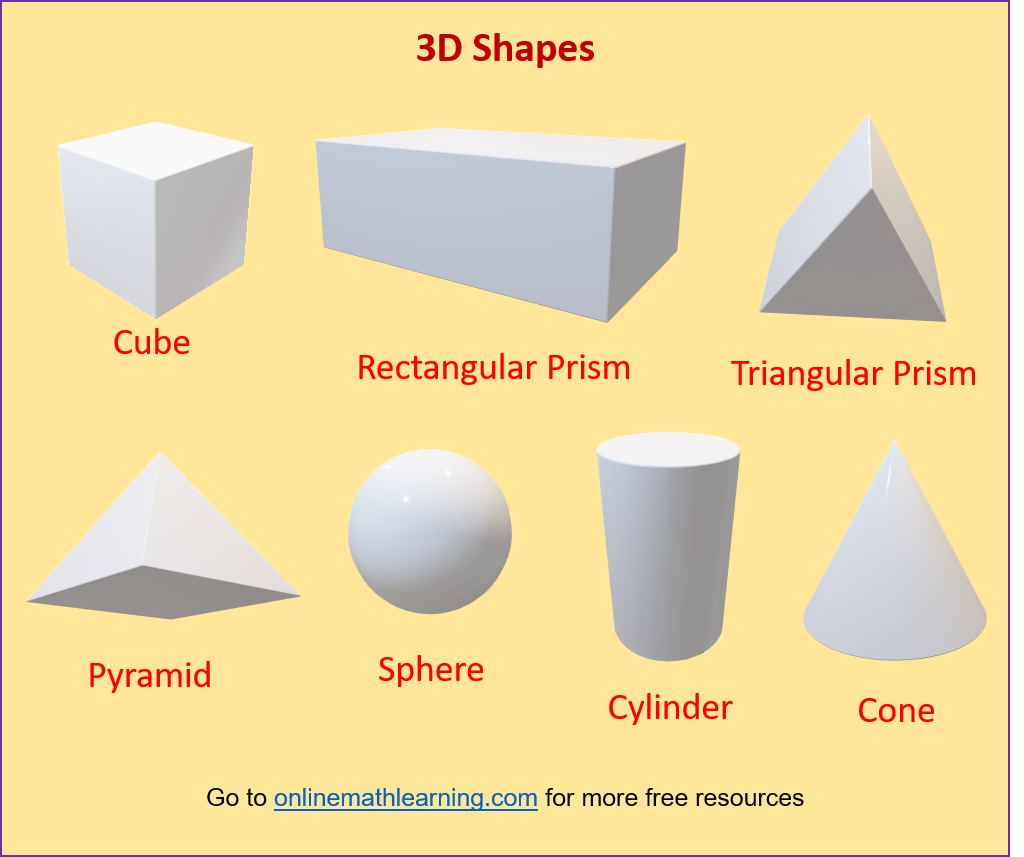
2D and 3D Shapes Worksheets
Printable
Recognizing 2D Shapes (Kindergarten)
Recognizing 3D Shapes (Kindergarten)
Drawing 2D Shapes (Kindergarten)Sides & Corners (First Grade)
2D Shapes (First Grade)
Divide Shapes (Halves & Quarters)Shapes & Attributes (2nd Grade)
Polygons (2nd Grade)
Quadrilaterals (2nd Grade)
Composite Shapes (2nd Grade)
Divide Composite Shapes (2nd Grade)
Divide Circles & Rectangles
Relate Square to Cube (2nd Grade)Classify Quadrilaterals (3rd Grade)
Classify Polygons (3rd Grade)Lines of Symmetry
Types of Triangles
Classify Quadrilaterals (4th & 5th Grade)Online
Quadrilateral Properties
Angles in a QuadrilateralAngles in Polygons
Interior Angles in Polygons
Exterior Angles in Polygons
Pyramid
A face is a surface on a geometric object. An edge occurs when two faces of a 3-D object meet. A vertex is a point where three or more edges meet. In a pyramid, the vertex is the highest point above a base.
A pyramid has one base. The base is a special face that determines the name of the pyramid. The remaining faces in a pyramid are always triangles that meet at one point or vertex.
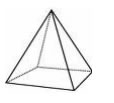
A pyramid with a square base is a square pyramid. A square pyramid has 5 faces, 8 edges and 5 vertices.
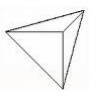
A pyramid with a triangular base is a triangular pyramid. A triangular pyramid has 4 faces, 6 edges and 4 vertices.
Prism
A prism has 2 bases that are matching polygons. The 2 bases are special faces that determine the name of the prism. The other faces are rectangles.
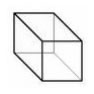
A prism with 2 rectangular bases is a rectangular prism. A rectangular prism has 6 faces, 12 edges and 8 vertices.
Note that a cube is a special rectangular prism with 6 equal square faces.
A prism with 2 triangular bases is a triangular prism. A triangular prism has 5 faces, 9 edges and 6 vertices.
Cylinder, Cone, Sphere
A cylinder is a 3-D object with 2 flat faces (which are circles), 1 curved face, 2 edges and 0 vertices.
A cone is a 3-D object with 1 flat face (which is a circle), 1 curved face, 1 edge and 1 vertex.
A sphere is a 3-D object with 1 curved face, 0 edges and 0 vertices.
3D-shapes: Faces, vertices and edges
How to find edges and vertices. Cubes, triangular pyramids, square based pyramids, and an explanation of edges, vertices and faces.
Nets of 3-D Objects
A net can be described as a ‘jacket’ for a geometric solid that can be folded to cover or create the surface of the solid. A net is a two-dimensional figure with indicated lines for folding to create a three-dimensional solid.
Geometric nets are matched with their corresponding shapes. Movies of the folding of the geometric nets are included.
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
Penguin Solitaire:
Move all cards to the foundations to build four full sequences. There are two versions here: Penguin (Tuxedo) and Penguin (Original).
Sawayama Solitaire:
This is similar to the common Klondike Solitaire except for a few changes to make it more strategic.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.