Volume Of A Cone
Related Pages
Volume Formulas
Volume Formulas Explained
Surface Area Formulas
More Geometry Lessons
In these lessons, we will learn:
- what a cone is
- how to calculate the volume of a cone.
- how to solve word problems about cones.
- how to prove the formula of the volume of a cone.
Volume of a cone
The volume of a cone measures how much space it occupies. The formula is derived from the volume of a cylinder, with an adjustment for the cone’s tapering shape. A cone’s volume is exactly one-third the volume of a cylinder with the same base radius and the same height.
Formula for the Volume of a Cone
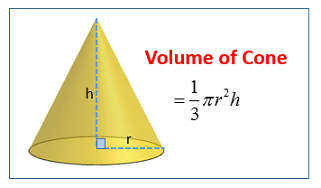
The following diagram shows the formula for the volume of a cone. Scroll down the page for
more examples and solutions on how to use the formula.
Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets
The formula for the volume (V) of a cone is given by:
\(V = \frac{1}{3} π r^2 h \)
Where:
V = Volume of the cone
π (pi) is a mathematical constant, approximately 3.142.
r = radius of the circular base of the cone.
h = height of the cone (the perpendicular distance from the apex, or tip, of the cone to the center of its circular base)
Explanation of the Formula Components
πr2: This part of the formula calculates the area of the circular base of the cone.
h: This is the height of the cone.
\(\frac{1}{3}\): A cone’s volume is exactly one-third the volume of a cylinder that has the same base radius and the same height.
Cones
A cone is a solid with a circular base. It has a curved surface which tapers (i.e. decreases in size) to a vertex at the top. The height of the cone is the perpendicular distance from the base to the vertex.
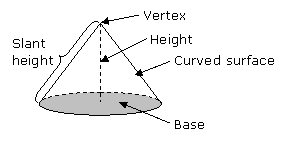
A right cone is a cone in which the vertex is vertically above the center of the base. When the vertex of a cone is not vertically above the center of the base, it is called an oblique cone.
The following diagrams show a right cone and an oblique cone.

In common usage, cones are assumed to be right and circular. Its vertex is vertically above the center of the base and the base is a circle. However, in general, it could be oblique and its base can be any shape. This means that technically, a cone is also a pyramid.
Volume Of A Cone
The volume of a right cone is equal to one-third the product of the area of the base and the height.
It is given by the formula:
![]()
where r is the radius of the base and h is the perpendicular height of the cone.
Worksheet For Volumes Of Cones.
Example:
Calculate the volume of a cone if the height is 12 cm and the radius is 7 cm.
Solution:
Volume of the cone
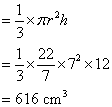
How To Use The Formula To Find The Volume Of A Cone?
This video lesson provides an example of how to determine the volume of a cone.
How To Solve Word Problems Involving Cones?
Example:
A Maxicool consists consists of a cone full of ice-cream with a hemisphere of ice-cream on top.
The radius of a hemisphere is 3 cm. The height of the cone is 10 cm. Calculate the total volume
of the ice-cream.
Example:
A scoop of strawberry of radius 5 cm is placed in a cone. When the ice-cream melts, it fills two
thirds of the cone. Find the volume of the cone. (Assuming no ice-cream drips outside the cone).
Proof For The Formula Of The Volume Of A Cone
This video will demonstrate that the volume of a cone is on-third that of a cylinder with the same base and height. This is not a formal proof. You would need to use calculus for a more rigorous proof.
Using Calculus To Derive The Volume Of A Cone (Integral)
We use integration to deduce the formula for the volume of a cone.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.