A Tangled Tale - Answer to Knot I

Related Topics:
More Lessons for Math Trivia
Math Worksheets

Answer: 24 miles: half-past 6.

Solution: A level mile takes 1/4 of an hour, up hill 1/3, down hill 1/6. Hence to go and return over the same mile, whether on the level or on the hillside, takes 1/2 an hour. Hence in 6 hours they went 12 miles out and 12 back. If the 12 miles out had been nearly all level, they would have taken a little over 3 hours; if nearly all up hill, a little under 4. Hence 3½ hours must be within a an hour of the time taken in reaching the peak; thus, as they started at 3, they got there within 1/2 an hour of 1/2 past 6

Lewis Carroll's replies to correspondents:
The two wrong answers are from Gerty Vernon and A Nihilist. The former makes the distance “23 miles”, while her revolutionary companion puts it at “27” Gerty Vernon says, “they had to go 4 miles along the plain, and got to the foot of the hill at 4 o’clock.” They might have done so, I grant; but you have no ground for saying they did so. “It was 7½ miles to the top of the hill, and they reached that at 1/4 before 7 o’clock.” Here you go wrong in your arithmetic, and I must, however reluctantly, bid you farewell. 7½ miles, at 3 miles an hour, would not require 2 3/4 hours. A Nihilist says, “let x denote the whole number of miles; y the number of hours to hill-top; 3y = number of miles to hill-top, and x-3y = number of miles on the other side.” You bewilder me. The other side of what? “Of the hill,” you say. But then, how did they get home again? However, to accommodate your views we will build a new hostelry at the foot of the hill on the opposite side, and also assume (what I grant you is possible, though it is not necessarily true) that there was no level road at all. Even then you go wrong. You say:

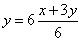…(i)

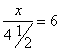…(ii)

I grant you (i), but I deny (ii): it rests on the assumption that to go part of the time at 3 miles an hour, and the rest at 6 miles an hour, comes to the same result as going the whole time at 4½ miles an hour. But this would only be true if the “part” were in exact half, i.e. if they went up hill for 3 hours, and down hill for the other 3: which they certainly did not do.

The sixteen who are partially right, are Agnes Bailey, F. K. Fifee, G. E. B., H. P., Kit, M. E. T., Mysie, A Mother’s Son, Nairam, A Redruthian, A Socialist, Spear Maiden, T. B. C., Vis Inertiae, and Yak. Of these, F. K., Fifee, T. B. C., and Vis Inertiae do not attempt the second part at all. F. K. and H. P. give no working. The rest make particular assumptions, such as that there was no level road — that there were 6 miles of level road — and so on, all leading to particular times being fixed for reaching the hill-top. The most curious assumption is that of Agnes Bailey, who says, “Let x = number of hours occupied in ascent; then x/2 = hours occupied in descent; and 4x/3 = hours occupied on the level.” I suppose you were thinking of the relative rates, up hill and on the level; which we might express by saying that, if they went x miles up hill in a certain time, they would go 4x/3 miles on the level in the same time. You have, in fact, assumed that they took the same time on the level that they took in ascending the hill. Fifee assumed that, when the aged knight said they had gone “four miles in the hour” on the level, he meant that four miles was the distance gone, not merely the rate. This would have been — if Fifee will excuse the slang expression — a “sell”, ill-suited to the dignity of the hero.

And now, “descend, ye classic Nine!” who have solved the whole problem, and let me sing your praises. Your names are Blithe, E. W., L. B., A Marlborough Boy, O. V. L., Putney Walker, Rose, Sea-Breeze, Simple Susan, and Money-Spinner. (These last two I count as one, as they send a joint answer.) Roe and Simple Susan and Co. do not actually state that the hill-top was reached sometime between 6 and 7, but, as they have clearly grasped the fact that a mile, ascended and descended, took the same time as two level miles, I mark them as “right”. A Marlborough Boy and Putney Walker deserve honourable mention for their algebraic solutions, being the only two who have perceived that the question leads to an indeterminate equation. E. W. brings a charge of untruthfulness against the aged knight — a serious charge, for he was the very pink of chivalry! She says, “According to the data given, the time at the summit affords no clue to the total distance. It does not enable us to state precisely to an inch how much level and how much hill there was on the road.” “Fair damsel,” the aged knight replies, “ — if, as I surmise, thy initials denote Early Womanhood — bethink thee that the word ‘enable’ is thine, not mine. I did but ask the time of reaching the hill-top as my condition for further parley. If now thou wilt not grant that I am a truth-loving man, then will I affirm that those same initials denote Envenomed Wickedness!”

Class List

1st place: A Marlborough Boy, Putney Walker.

2nd place: Blithe, Rose, E.W., Sea-Breeze, L.B., Simple Susan., O. V. L., Money-Spinner.

Blithe has made so ingenious an addition to the problem, and Simple Susan and Co. have solved it in such tuneful verse, that I record both their answers in full. I have altered a word or two in Blithe’s which I trust she will excuse; it did not seem quite clear as it stood.

Blithe's Answer:

“Yet say,” said the youth, as a gleam of inspiration lighted up the relaxing muscles of his quiescent features. “Stay. Methinks it matters little when we reached that summit, the crown of our toil. For in the space of time wherein we clambered up one mile and bounded down the same on our return, we could have trudged the twain on the level. We have plodded, then, four-and-twenty miles in these six mortal hours; for never a moment did we stop for catching of fleeting breath or for gazing on the scene around!”

“Very good,” said the old man. “Twelve miles out and twelve miles in. And we reached the top sometime between six and seven of the clock. Now mark me! For every five minutes that had fled since six of the clock when we stood on yonder peak, so many miles had we toiled upwards on the dreary mountain-side!”

The youth moaned and rushed into the hostel.

Simple Susan and Money Spinner's Answer:

The elder and the younger knight
They sallied forth at three;
How far they went on level ground
It matters not to me;
What time they reached the foot of hill,
When they began to mount,
Are problems which I hold to be
Of very small account.

The moment that each waved his hat
Upon the topmost peak —
To trivial query such as this
No answer will I seek.
Yet can I tell the distance well
They must have travelled o’er:
On hill and plain, ‘twixt three and nine,
The miles were twenty-four.

Four miles an hour their steady pace
Along the level track,
Three when they climbed — but six when they
Came swiftly striding back
Adown the hill; and little skill
It needs, methinks, to show,
Up hill and down together told,
Four miles an hour they go.

For whether long or short the time
Upon the hill they spent,
Two thirds were passed in going up,
One third in the descent.
Two thirds at three, one third at six,
If rightly reckoned o’er,
Will make one whole at four — the tale
Is tangled now no more.

Ready for Knot II?

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.