

Second Derivative
More Lessons for Calculus
Math Worksheets
Second Derivative
If f' is the differential function of f, then its derivative f'' is also a function. The new function f'' is called the second derivative of f because it is the derivative of the derivative of f. Using the Leibniz notation, we write the second derivative of y = f(x) as
![]()
We can interpret f ‘’(x) as the slope of the curve y = f(‘(x) at the point (x, f ‘(x)). In other words, it is the rate of change of the slope of the original curve y = f(x). In general, we can interpret a second derivative as a rate of change of a rate of change. The most common example of this is acceleration.
Example:
The position of a particle is given by the equation
s = f(t) = t3 – 4t2 + 5t
where t is measured in seconds and s in meters.
a) Find the velocity function of the particle
b) Find the acceleration function of the particle.
Solution:
a) The velocity function is the derivative of the position function.
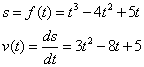
b) The acceleration function is the derivative of the velocity function
![]()

How to use the second derivative test to identify the presence of a relative maximum or a relative minimum at a critical point? If the second derivative is positive at a critical number - a local minimum is present. If the second derivative is negative at a critical number - a local maximum is present.
To identify the relative extrema:
1. Find the first derivative, set it equal to zero and identify the critical numbers.
2. Plug the critical numbers into the second derivative function to determine the concavity of the function to see if its concave up or concave down. If it's concave up - it's a relative maximum. If it's concave down, it's a relative minimum. You can confirm the results of the second derivative test using the first derivative test with a sign chart on a number line.
Example:
If f(x) = x cos x, find f ‘’(x).
Solution:
Using the Product Rule, we get
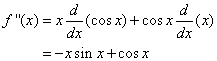
To find f ‘’(x) we differentiate f ‘(x):
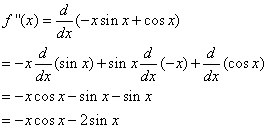
Higher Derivatives
The third derivative f ‘’’ is the derivative of the second derivative. The third derivative can be interpreted as the slope of the curve or the rate of change of the second derivative.
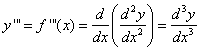
The process can be continued. The fourth derivative is usually denoted by f(4). In general the nth derivative of f is denoted by f(n) and is obtained from f by differentiating n times.
![]()
Examples of using the second derivative to determine where a function is concave up or concave down. Using Implicit Differentiation to find a Second Derivative
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.