SAT Practice Test 1, Section 3: Questions 16 - 20

16. Correct answer: (E)

Given:
Cylinder with radius x and height 2x

To find:
Which of the following has the same volume as given cylinder

Solution:
Topic(s): Volume of cylinder

Formula for volume of cylinder is
From the diagram, r = x and h = 2x
Volume of cylinder =
We now have to test each answer to determine which has the same volume as

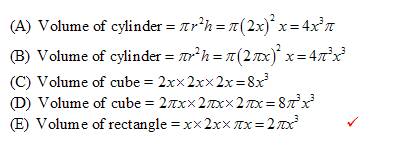
We found a match in (E).

You will notice that it is usually a good idea to start testing the answers from (E).

Answer: (E)

17. Correct answer: (B)

Given:
a + 2(x + 1) = s

To find:
x + 1, in terms of s and a

Solution:
Topic(s): Isolate variable

You are asked to solve for x + 1, and not for x, so isolate x + 1

2(x + 1) = s – a

Answer: (B)

18. Correct answer: (D)

Given:
The shaded region bounded by:
x-axis
line x = 4
y = f(x)

Point (a, b) lies in the shaded region

To find:
Which of the following must be true

Solution:
The shaded region is to the left of the vertical line x = 4.
So, condition I. a ≤ 4 is true.
The shaded region is below the graph y = f(x).
So, condition III. b ≤ f(a) is true.

In order for condition II. b ≤ a to be true, the shaded area must be below or on the line y = x. This would be a straight line passing through (0,0) and (4,4). We can see from the diagram that this is not always true.

Answer: (D) I and III only

19. Correct answer: (C)

Given:
Machine B only accepts the bottle if the fluid is between

To find:
The expression that describes all possible values of n

Solution:
Topic(s): Translating words to equations

From the question, you will get the following inequality for n:

Subtract 12 from each part of the inequality

Answer: (C)

20. Correct answer: (E)

Given:
The least integer of a set of consecutive integers is –25
The sum of these integers is 26

To find:
The number of integers in the set

Solution:
Topic(s): Consecutive numbers

The set of consecutive numbers from –25 to 25 is
–25, –24, …–1, 0, 1, …, 24, 25.

If we were to add the set of consecutive numbers from –25 to 25 we would get 0.

We now need to find out how many more numbers to add to get to a sum of 26. The number after 25 is 26, which is our required sum.

There are 51 numbers from –25 to 25 (don’t forget to count 0). If we include the number 26, we will have a total of 52 numbers.

Answer: (E) 52

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.