Median, Quartiles And Percentiles (Ungrouped Data)
In these lessons, we will learn how to find the median, quartiles and percentiles of ungrouped data (discrete data).
Related Pages
Frequency Table
Cumulative Frequency Graph
More Statistics Lessons
We have learned that the median is the middle value when a set of data is arranged in order of increasing magnitude. We will now consider lower quartiles and upper quartiles.
The median divides the data into a lower half and an upper half.
The lower quartile is the middle value of the lower half.
The upper quartile is the middle value of the upper half.
The following figure shows the median, quartiles and interquartile range. Scroll down the page for examples and solutions.
How To Find Median, Quartiles And Percentiles?
Example:
Find the median, lower quartile and upper quartile of the following numbers.
12, 5, 22, 30, 7, 36, 14, 42, 15, 53, 25
Solution:
First, arrange the data in ascending order:
Median (middle value) = 22
Lower quartile (middle value of the lower half) = 12
Upper quartile (middle value of the upper half) = 36
If there is an even number of data items, then we need to get the average of the middle numbers.
Example:
Find the median, lower quartile, upper quartile, interquartile range and range of the following numbers.
12, 5, 22, 30, 7, 36, 14, 42, 15, 53, 25, 65
Solution:
First, arrange the data in ascending order:
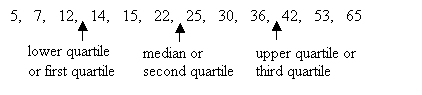
Lower quartile or first quartile = 
Median or second quartile = 
Upper quartile or third quartile = 
Interquartile range = Upper quartile – lower quartile
= 39 – 13 = 26
Range = largest value – smallest value
= 65 – 5 = 60
When evaluating the quartiles, always remember to first arrange the data in increasing order.
How to compute the interquartile range for a set of data?
Remember to reorganize the data so that you can find the median values easier.
Median, Quartiles and Interquartile Range
How to calculate median, quartiles and interquartile range for discrete data.
How to summarize data using quartiles and interquartile range?
How to Estimate Mean, Median and Quartiles from Continuous Grouped Data?
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.