Determinant of a 3x3 Matrix
These lessons, with videos, examples, and solutions, help Algebra students learn how to find the determinant of a 3×3 matrix.
Related Pages
Inverse of a 2×2 Matrix
Inverse Matrix
Determinant of a 2×2 Matrix
Matrices
More Lessons for Grade 9
How to evaluate a determinant using row operations?
How to calculate the determinant using the diagonal method and cofactor method?
3×3 Determinant
Methods for computing a 3×3 determinant are important and are used when defining the cross product. Finding a 3×3 determinant is not as computationally heavy as finding the determinant of a larger square matrix. However, finding this determinant is more complicated than finding a 2x2 determinant. Using methods for simplifying determinants through row operations can make finding the 3x3 determinant much simpler.
The following diagram shows how to evaluate a Determinant using Elementary Row Operations. Scroll down the page for more examples and solutions on how to find the determinant of matrices.
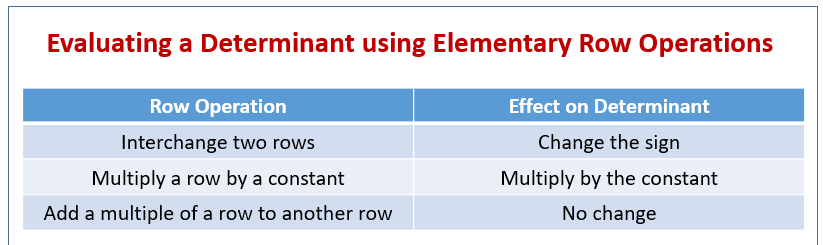
Evaluating a Determinant Using Elementary Row Operations
How to evaluate 2x2 and 3x3 determinants using the diagonal method and cofactor method.
Example of how to calculate the determinant using the diagonal method.
Example of how to calculate the determinant using the diagonal method
Example of how to calculate the determinant using the cofactor method.
Example of how to calculate the determinant using the cofactor method.
Finding the Determinant of a 3×3 matrix.
This video shows the basic formula and compute the determinant of a specific matrix.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.