SAT Practice Test 2, Section 3: Questions 16 - 20

Related Topics:
More Lessons for SAT Test Preparation

Math Worksheets

Related Topics:
More Lessons for SAT Preparation

Math Worksheets

This is for SAT in Jan 2016 or before.

The following are worked solutions for the questions in the math sections of the SAT Practice Tests found in the The Official SAT Study Guide Second Edition.

It would be best that you go through the SAT practice test questions in the Study Guide first and then look at the worked solutions for the questions that you might need assistance in. Due to copyright issues, we are not able to reproduce the questions, but we hope that the worked solutions will be helpful.

11. Correct answer: (A)

Given:

To find:

Solution:

Translate ‘of’ as ‘×’

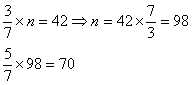
Answer: (A) 70

12. Correct answer: (E)

Given:
A square box is divided into 6 compartments
Each of the rectangles D, E and F has twice the area of each of the equal squares A, B and C

To find:
The probability that a marble dropped will fall into compartment F

Solution:
Topic(s): Probability

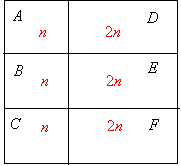
If we take the areas of A, B and C to be n each then the areas of D, E and F will be 2n.

Altogether, the areas would be n + n + n + 2n + 2n +2n = 9n

Area of F = 2n

Probabilty of it falling in F would be

Answer: (E)

13. Correct answer: (E)

Given:
a and b are odd integers

To find:
The expression(s) that must be odd integer(s)

Solution:
Topic(s): Even and odd numbers

Refer to the rules regarding operations on even and odd numbers

Since a is an odd numbers then, a + 1 is even

Check out each of the statement to find out which gives an odd number:

I. (a + 1) b → Even × Odd = Even (no)

II. (a + 1) + b → Even + Odd = Odd (yes)

III. (a + 1) – b → Even – Odd = Odd (yes)

Answer: (E) II and III

14. Correct answer: (D)

Given:
The decimal number 5.1011001000100001 …
After the decimal point, the first 1 is followed by one 0
the second 1 is followed by two 0’s and so on

To find:
Total number of 0’s between the 98th to the 101st ones

Solution:
Topic(s): Number sequence problem

Try to detect the pattern

After 1st one → 1 zero
After 2nd one → 2 zeros
.
.
.
After 98th one → 98 zeros
After 99th one → 99 zeros
After 100th one → 100 zeros
(Stop here; do not include the zeros after 101st one)

Total number of zeros from 98th one to 101st one is 98 + 99 + 100 = 297

Answer: (D) 297

15. Correct answer: (D)

Given:
f(x) =

To find:
The value of f(2)

Solution:
Substitute x = 2 into

Answer: (D)