Equation Of A Line
In these lessons, we will learn
- the slope-intercept form for the equation of a line.
- how to write equations in slope-intercept form.
- how to write equations of horizontal and vertical lines.
- how to get the equation of a line given two points on the line.
- how to graph an equation using the slope-intercept form.
Related Pages
Coordinate Plane
More Geometry Lessons
Slope-Intercept Form
The equation, y = mx + b, is in slope-intercept form for the equation of a line. When an equation is in this form, the slope of the line is given by m and the y-intercept is located at b.
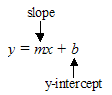
For example, a line with the equation y = 2x + 4 has a slope of 2 and a y-intercept of 4.
The following diagram shows an equation in slope-intercept form. Scroll down the page for more examples and solutions on how to use the slope-intercept form of an equation.
-
Linear Equation Worksheets
Linear Equations & Coordinate Plane
Slope of a Line (from 2 points)
Slope of a Line (from equation)
Graph Equation using Intercepts
Find the Equation of a Line
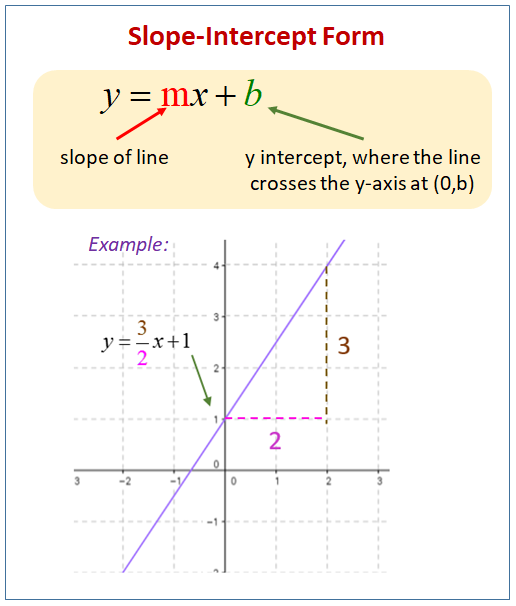
Slope and y-intercept of an equation
How To Write Equations In Slope-Intercept Form?
The slope-intercept from is useful when we want to find the slope or y-intercept of an equation. To write an equation in slope-intercept form, we isolate the y on one side of the equation.
The following video shows how to change a linear equation into slope-intercept form.
A linear equation written in the form y = mx + b is in slope intercept form where m is the slope and b is the y intercept of the line.
Example:
Write the equation -3x + 4y = 8 in slope intercept form. State the slope and y intercept.
How to find the slope and y-intercept of line by writing the equation in slope-intercept form?
Examples:
Find the slope:
y = -3x + 8
3x - 5y = 10
y = 5
x = -2
How to find the slope and y-intercept for a linear equation?
Examples:
Find the slope and y-intercept for the linear equation.
a) y = -2x + 3
b) y = 4 - 2/3 x
c) 2x - 5y = 10
d) 3x + 7y - 10 = 0
e) 8y + 24 = 0
Equations Of Horizontal And Vertical Lines
A horizontal line has a slope of zero which means that m = 0. The equation of a horizontal line is then in the form
y = 0x + b which is the same as y = b, where b is the y-intercept.
A vertical line has a slope that is undefined. Therefore, it cannot be written in slope-intercept form. Instead, the equation of a vertical line is in the form
x = a, where a is the x-intercept.
How to write the equation of vertical and horizontal lines?
Writing the Equation of a Line from Two Points
To find the equation of a line when given two points on the line, we first find the slope and then find the y-intercept.
The slope is the ratio of the change in the y-value over the change in the x-value. Given any two points on a line, you can calculate the slope of the line by using this formula:
Example:
Given two points, P = (0, –1) and Q = (4,1), on the line, find the equation of the line.
Solution:
Step 1: Calculate the slope.
slope = 
= 
Step 2: Substitute m = 
,
into the equation, y = mx + b, to get the equation 
Step 3: Select one of the given points, for example (4, 1), and substitute the x and y values into the equation.
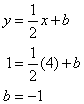
We, then, get that b = −1, which is the y-intercept.
Step 4: Substitute b = −1 to get the equation.
y = x − 1
How to determine the equation of a line in slope-intercept form given two points on the line?
Example:
Determine the equation of the line passing through (-2, -3) and (4, -2). Write the linear equation
in slope-intercept form.
Examples of getting the slope and y-intercept given two points and then obtaining the equation of the line.
How To Graph An Equation Using The Slope-Intercept Form?
This video explains how to graph a linear equation given in slope intercept form.
Example:
Identify the slope and y-intercept. Graph.
a) y = -2/3 x + 1
b) y = 5x - 2
c) y = x
d) 3x - 2y = 8
How to graph a linear equation using the slope and y-intercept?
Examples:
- Graph the line y = -2/3 x + 4
- Graph the line y = 3x + 2
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.