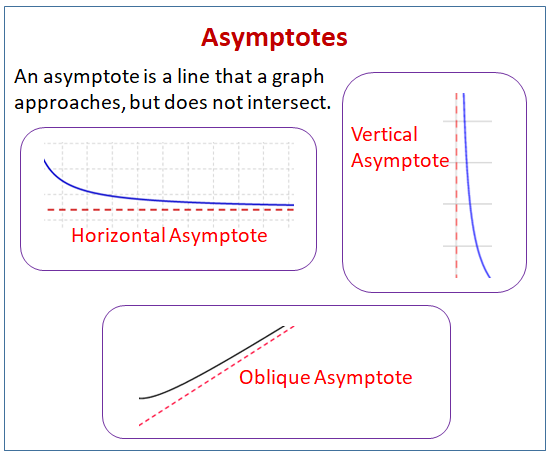
Calculus: Asymptotes
An asymptote is a line that a graph approaches, but does not intersect.
In these lessons, we will learn how to find vertical asymptotes, horizontal asymptotes and oblique (slant) asymptotes of rational functions.
Related Pages
Reciprocal Functions
Hyperbolas
More lessons on Calculus
The following diagram shows the different types of asymptotes: horizontal asymptotes, vertical asymptotes, and oblique asymptotes. Scroll down the page for more examples and solutions on how to find asymptotes.
Vertical Asymptote
How to determine the Vertical Asymptote?
Method 1: Use the Definition of Vertical Asymptote
The line x = a is called a Vertical Asymptote of the curve y = f(x) if at least one of the following statements is true.
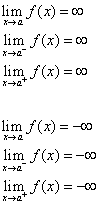
Method 2:
For rational functions, vertical asymptotes are vertical lines that correspond to the zeroes of the denominator.
Given the rational function, f(x)
Step 1: Write f(x) in reduced form
Step 2: if x – c is a factor in the denominator then x = c is the vertical asymptote.
Example:
Find the vertical asymptotes of 
Solution:
Method 1: Use the definition of Vertical Asymptote.
If x is close to 3 but larger than 3, then the denominator x – 3 is a small positive number and 2x is close to 8. So, is a large positive number.
Intuitively, we see that
Similarly, if x is close to 3 but smaller than 3, then x – 3 is a small negative number and 2x is close to 8. So, 
is a large negative number.
The line x = 3 is the vertical asymptote.
Method 2:
Step 1: f(x) is already in reduced form.
Step 2: The denominator is x – 3, and so the Vertical Asymptote is at x = 3.
Finding Vertical Asymptotes of Rational Functions
What to look for, in order to find vertical asymptotes of rational functions.
Vertical Asymptotes of Rational Functions: Quick Way to Find Them
Example of finding vertical asymptotes of rational functions.
Horizontal Asymptote
How to determine the horizontal Asymptote?
Method 1: Use the definition of Horizontal Asymptote
The line y = L is called a horizontal asymptote of the curve y = f(x) if either
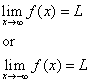
Method 2:
For the rational function, f(x)
If the degree of x in the numerator is less than the degree of x in the denominator then y = 0 is the horizontal asymptote.
If the degree of x in the numerator is equal to the degree of x in the denominator then y = c where c is obtained by dividing the leading coefficients.
Example:
Find the horizontal and vertical asymptotes of the function.
Solution:
Method 1:
Divide both numerator and denominator by x.
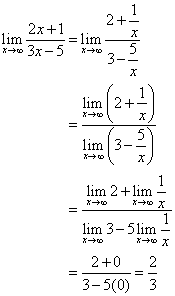
The line 
is the horizontal asymptote.
Method 2:
The degree of x in the numerator is equal to the degree of x in the denominator.
Dividing the leading coefficients we get 
The line is the horizontal asymptote.
Shortcut to Find Horizontal Asymptotes of Rational Functions
A couple of tricks that make finding horizontal asymptotes of rational functions very easy to do
The degree of a function is the highest power of x that appears in the polynomial. To find the horizontal asymptote, there are three easy cases.
- If the degree of the numerator expression is less than the degree of the denominator expression, then the horizontal asymptote is y=0 (the x-axis).
- If the degree of the numerator is equal to the degree of the denominator, then you can find the horizontal asymptote by dividing the first, highest term of the numerator by the first, highest term of the denominator. This will simplify to y = some constant (just a number).
- If the degree of the numerator is greater than the degree of the denominator, then there is no horizontal asymptote.
Oblique Asymptote or Slant Asymptote
Some curves have asymptotes that are oblique, that is, neither horizontal nor vertical.
If 
then the line y = mx + b is called the oblique or slant asymptote because the vertical distances
between the curve y = f(x) and the line y = mx + b approaches 0.
For rational functions, oblique asymptotes occur when the degree of the numerator is one more than the degree of the denominator. In such a case the equation of the oblique asymptote can be found by long division.
Example:
Find the asymptotes of the function 
Solution:
Since the denominator x2 + 1 is never 0, there is no vertical asymptote.
Since the degree of x in the numerator is greater than the degree of x in the denominator there is no horizontal asymptote.
Since the degree of x in the numerator is one greater than the degree of x in the denominator we can use long division to obtain the oblique asymptote.
So, the line y = x is the oblique asymptote.
Finding Slant Asymptotes of Rational Functions
This video describes when a rational function has a slant asymptote, briefly describe what a slant asymptote is, and then do two examples.
Find Asymptotes of a Rational Function (Vertical, Horizontal and Oblique/Slant)
This video shows how to find the vertical asymptotes and a slant / oblique asymptotes of a rational function.
Finding All Asymptotes of a Rational Function (Vertical, Horizontal, Oblique / Slant)
Here we look at a function and find the vertical asymptote and also conclude that there are no horizontal asymptotes, but that an oblique asymptote does exist. We then use long division to find the oblique asymptote.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.