Area Of A Triangle Using Sine
In these lessons, we will learn how to find the area of a triangle using the sine function when given side-angle-side (SAS).
Related Topics:
More Trigonometric Lessons
More Geometry Lessons
The most common formula for the area of a triangle would be:
Area = ½ × base(b) × height (h)
Another formula that can be used to obtain the area of a triangle uses the sine function. It allows us to find the area of a triangle when we know the lengths of two sides and the size of angle between them.
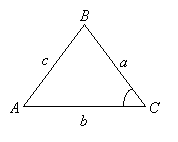
The formula is
Area of triangle = ½ ab sinC
Remember that the given angle must be between the two given sides.
Example:
Find the area of triangle PQR if p = 6.5 cm, r = 4.3 cm and ∠ Q = 39˚. Give your answer correct to 2 decimal places.
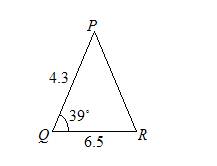
Solution:
Area of triangle PQR
= ½ pr sinQ
= ½ × 6.5 × 4.3 × sin 39˚
= 8.79 cm2
Example:
In triangle ABC if AC = 2BC and ∠ C = 112˚. The area of triangle ABC is 16.3 cm Find the length of BC . Give your answer correct to 2 significant figures.
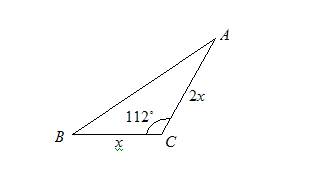
Solution:
Let the length of BC = x
and the length of AC = 2x
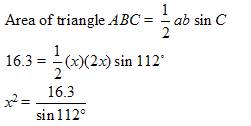
x = 4.19 cm
So, BC = 4.2 cm
Videos
The Area of a Triangle using Sine
This video explains how to determine the area of a triangle using the sine function when given side-angle-side (SAS).
Example:
- Determine the area of the following triangle:
a) A = 35°, B = 82°, a = 6 cm, b = 15 cm
b) B = 72°, a = 23.7 ft, b = 35.2 ft.
Determine the Area of a Triangle Using the Sine Function
This video provides an example of how to determine the area of a triangle using the sine function.
How to use the sine function to find the area of a triangle?
Example:
Find the area of the oblique triangle with the given information
A = 100°, b = 14, c = 21
Area Triangles using Sine
This video explains how to find the area of a triangle using Sine.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.