Construct An Angle Bisector

Printable & Online Geometry Worksheets

An angle bisector is a straight line that divides the angle into two equal parts.

Example:
Construct an angle bisector for the following angle:

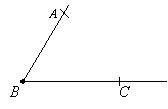
Solution:
Step 1: Put the sharp end of your compasses at point B and make one arc on the line BC (point S) and another arc on line AB (point T).

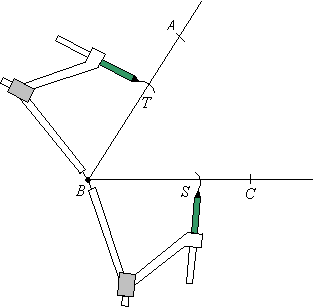
Step 2: Put the sharp end of the compasses at S and make an arc within the lines AB and BC. Do the same at T and make sure that the second arc intersects the first arc.

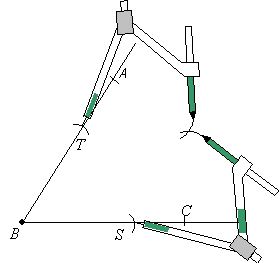
Step 3: Draw a line from point B to the points of intersection of the 2 arcs. This line bisects ∠ABC.

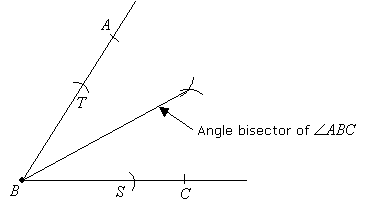
The steps to construct an angle bisector can be summarized as follows:

1. From the vertex, draw an arc across both rays of the angle.
2. From each arc intersection draw another pair of arcs that intersect each other.
3. Draw a line from the vertex to the intersection point to form the angle bisector.

How to draw an angle bisector using a compass and a straight edge?

1. Place compass point on the vertex, and draw an arc across each ray.
2. Place the compass on each arc intersection and draw a further pair of arcs which intersect each other.
3. Use a straight edge to connect the intersection point to the vertex.

• Show Video Lesson

How to bisect a given angle using only a compass and straightedge?

• Show Video Lesson

Use Angle Bisector To Construct Angles

We can use the angle bisector to construct some other angles from existing angles.

For examples:
A 30˚ angle can be obtained by bisecting a 60˚ angle.
A 15˚ angle can be obtained by bisecting a 30˚ angle.
A 45˚ angle can be obtained by bisecting a 90˚ angle.
A 22.5˚ angle can be obtained by bisecting a 45˚ angle.

Example:
The figure shows a point A on a straight line. Construct an angle of 45˚ at point A.

Solution:
Construct a 90˚ angle, and then construct an angle bisector to obtain a 45˚ angle.

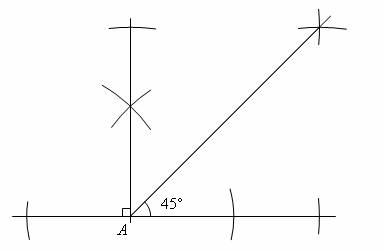
How to construct 30, 45, 60, 90, and 120 degree angles with a compass by constructing angle bisectors?

• Show Video Lesson

How to construct a 75° angle by constructing a 60° angle and a 15° angle?

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.