Work Word Problems - More Than Two Persons

Work Problems are word problems that involve different people doing work together but at different rates. If the people were working at the same rate then we would use the Inversely Proportional Method instead.

The formula for “Work” Problems that involve three persons is:

 

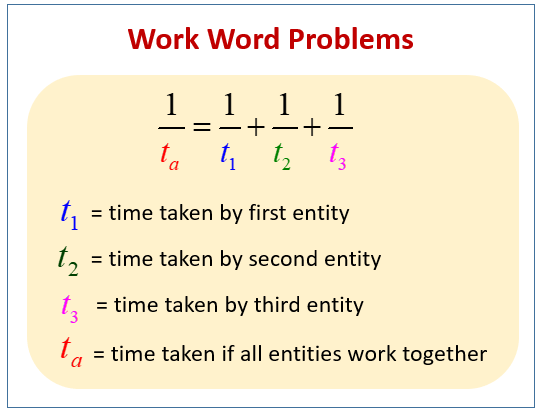
This formula can be modified for two or more persons. It can also be used in problems that involve pipes filling up a tank.

“Work” Problems: More Than Two Persons

Example:
Jane, Paul and Peter can finish painting the fence in 2 hours. If Jane does the job alone she can finish it in 5 hours. If Paul does the job alone he can finish it in 6 hours. How long will it take for Peter to finish the job alone?

Solution:
Step 1: Assign variables:
Let x = time taken by Peter

Step 2: Use the formula:

Step 3: Solve the equation
Multiply both sides with 30x

Answer: The time taken for Peter to paint the fence alone is hours.

How To Solve Work Word Problems?

It is possible to solve word problems when two people are doing a work job together by solving systems of equations. To solve a work word problem, multiply the hourly rate of the two people working together times the time spent working to get the total amount of time spent on the job. Knowledge of solving systems of equations is necessary to solve these types of problems.

Algebra Word Problems: Rates Of Performing Work

Example:
Jim can dig a hole by himself in 12 hours. John can do it in 8 hours. Jack can do it in 6. How long will it take them if they all work together?

• Show Video Lesson

How To Solve Work Word Problems With Three Persons?

Example:
If Amy, Bianca and Carrie work together on a job, it will take one and one-third hours. If only Amy and Bianca work, it would take one and five-sevenths hours, but if Bianca and Carrie work, it would take two and two-fifths hours, how long would it take each girl working alone to complete the job?

• Show Video Lesson

How To Solve Math Problems Involving Rates Of Work?

Example:
John can paint a garage in 8 hours. Gary can do it in 6 hours. Fred can do it in 4 hours. How long will it take if they all paint together?

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.