Value of a Ratio and Equivalent Ratios

Related Pages
Lesson Plans and Worksheets for Grade 6
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 6
Common Core For Grade 6

New York State Common Core Math Module 1, Grade 6, Lesson 8

Worksheets for Grade 6

Lesson 8 Student Outcomes

• Students understand the value of a ratio A:B is A/B. They understand that if two ratios are equivalent, the ratios have the same value.
• Students use the value of a ratio to solve ratio problems in a real-world context.
• Students use the value of a ratio in determining whether two ratios are equivalent.

The following diagram shows some examples of equivalent ratios. Scroll down the page for more examples and solutions on how to find equivalent ratios.

 

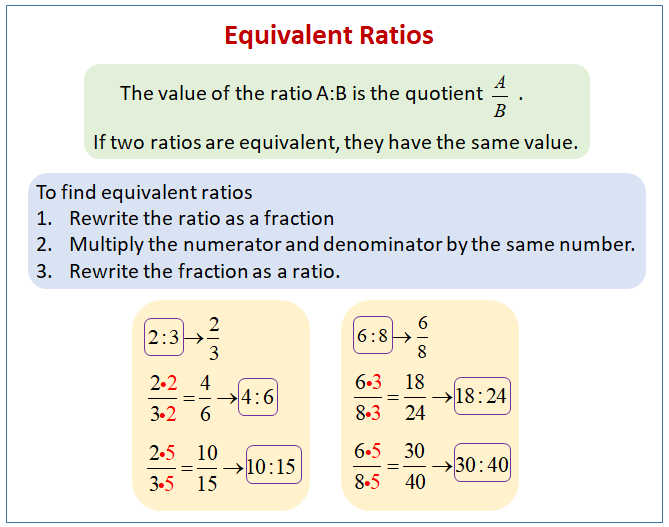
Lesson 8 Summary

The value of the ratio A:B is the quotient A/B
If two ratios are equivalent, they have the same value.

Grade 6, Module 1, Lesson 8: Classwork

Recall that when given a ratio A:B, where B ≠ 0, we call the quotient, A/B, the value of the ratio.

Exercise 1
Circle any equivalent ratios from the list below.
Ratio: 1:2
Ratio: 5:10
Ratio: 6:16
Ratio: 12:32

Find the value of the following ratios, leaving your answer as a fraction, but re-write the fraction using the largest possible unit.
Ratio: 1:2
Ratio: 5:10
Ratio: 6:16
Ratio: 12:32
What do you notice about the value of the equivalent ratios?

Exercise 2
Here is a theorem:
If two ratios are equivalent, then they have the same value. Can you provide any counter-examples to the theorem above?

Exercise 3
Taivon is training for a duathlon, which is a race that consists of running and cycling. The cycling leg is longer than the running leg of the race, so while Taivon trains, he rides his bike more than he runs. During training, Taivon runs 4 miles for every 14 miles he rides his bike.
a. Identify the ratio associated with this problem and find its value.

Use the value of each ratio to solve the following.
b. When Taivon completed all of his training for the duathlon, the ratio of total number of miles he ran to total number of miles he cycled was 80:280. Is this possible according to Taivon’s training schedule? Explain why or why not.

• Show Video Lesson

Problem Set

1. The ratio of the number of shaded sections to the number of unshaded sections is 4 to 2.
   What is the value of the ratio of the number of shaded pieces to the number of unshaded pieces?

2. Use the value of the ratio to determine which ratio(s) is equivalent to 7:15.
   a. 21:45
   b. 14:45
   c. 3:5
   d. 63:135

3. Sean was at batting practice. He swung 25 times but only hit the ball 15 times.
   a. Describe and write more than one ratio related to this situation.
   b. For each ratio you created, use the value of the ratio to express one quantity as a fraction of the other quantity.

• Show Video Lesson

Word Problems

Use the value of the ratio 6:20 to circle which of the ratios are equivalent to it.
a. 3:10
b. 12:24
c. 54:180

Your middle school has 700 students. One-fourth of the students get a ride to school everyday. What is the value of the number of students who get a ride to school to those that do not?

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.