

Unique Triangles—Two Sides and a Non-Included Angle
Related Topics:
Lesson Plans and Worksheets for Grade 7
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 7
Common Core For Grade 7
Videos, examples, solutions, and lessons to help Grade 7 students learn understand that two sides of a triangle and an acute angle, not included between the two sides, may not determine a unique triangle.
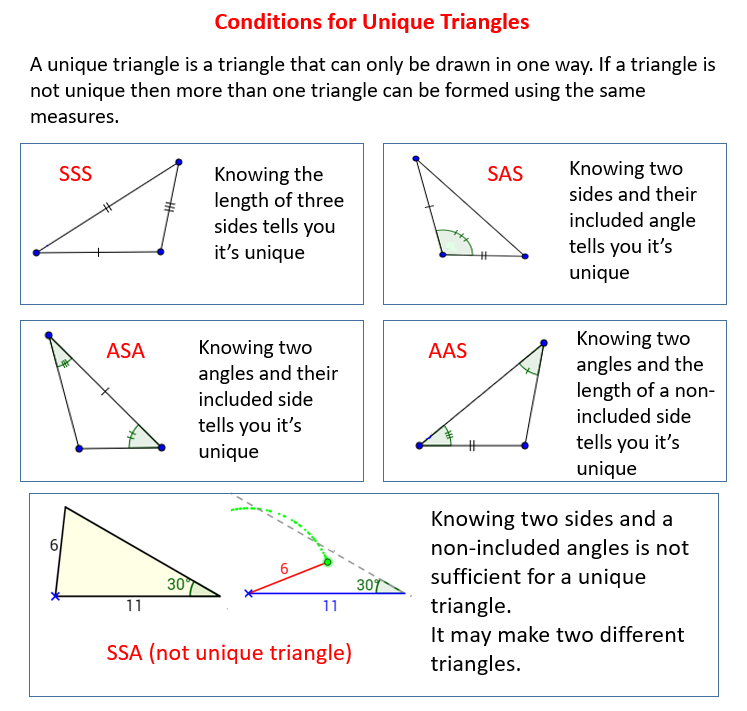
The following figures give the Conditions for a Unique Triangle - Side-Side-Angle (SSA). Scroll down the page for more examples and solutions.
• Students understand that two sides of a triangle and an acute angle, not included between the two sides, may not determine a unique triangle.
• Students understand that two sides of a triangle and a angle (or obtuse angle), not included between the two sides, determine a unique triangle.
• A triangle drawn under the condition of two sides and a non-included angle, where the angle is acute, does not determine a unique triangle. This condition determines two non-identical triangles.
• Consider a triangle correspondence △ABC ↔ △XYZ that corresponds to two pairs of equal sides and one pair of equal, non-included angles. If the triangles are not identical, then △ABC can be made to be identical to △XYZ by swinging the appropriate side along the path of a circle with a radius length of that side.
• A triangle drawn under the condition of two sides and a non-included angle, where the angle is 90° or greater, does determine a unique triangle.
Lesson 12 Classwork
Exploratory Challenge
1. Use your tools to draw △ABC, provided AB = 5 cm, BC = 3 cm, and ∠A = 30°. Continue with the rest of the problem as you work on your drawing.
a. What is the relationship between the given parts of △ABC?
b. Which parts of the triangle can be drawn without difficulty? What makes this drawing challenging?
c. A ruler and compass are instrumental in determining where C is located.
• Even though the length of AC is unknown, extend the ray AC in anticipation of the intersection with BC.
• Draw segment BC with length 3 cm away from the drawing of the triangle.
• Adjust your compass to the length of BC.
• Draw a circle with center B and a radius equal to BC, or 3 cm.
d. How many intersections does the circle make with AC? What does each intersection signify?
e. Complete the drawing of △ABC.
f. Did the results of your drawing differ from your prediction?
2. Now attempt to draw this triangle: draw △DEF, provided DE = 5 cm, EF = 3 cm, and ∠F = 90°.
a. How are these conditions different from those in Exercise 1, and do you think the criteria will determine a unique triangle?
b. What is the relationship between the given parts of △DEF?
c. Describe how you will determine the position of DE.
d. How many intersections does the circle make with FE?
e. Complete the drawing of △DEF. How is the outcome of △DEF different from that of △ABC?
f. Did your results differ from your prediction?
3. Now attempt to draw this triangle: draw △JKL, provided KL = 8 cm, KJ = 4 cm, and ∠J = 120°. Use what you drew in Exercises 1 and 2 to complete the full drawing.
4. Review the conditions provided for each of the three triangles in the Exploratory Challenge, and discuss the uniqueness of the resulting drawing in each case.


Lesson Plans and Worksheets for Grade 7
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 7
Common Core For Grade 7
Videos, examples, solutions, and lessons to help Grade 7 students learn understand that two sides of a triangle and an acute angle, not included between the two sides, may not determine a unique triangle.
New York State Common Core Math Grade 7, Module 6, Lesson 12
Worksheets for Grade 7The following figures give the Conditions for a Unique Triangle - Side-Side-Angle (SSA). Scroll down the page for more examples and solutions.
Lesson 12 Student Outcomes
• Students understand that two sides of a triangle and an acute angle, not included between the two sides, may not determine a unique triangle.
• Students understand that two sides of a triangle and a angle (or obtuse angle), not included between the two sides, determine a unique triangle.
Lesson 12 Summary
• A triangle drawn under the condition of two sides and a non-included angle, where the angle is acute, does not determine a unique triangle. This condition determines two non-identical triangles.
• Consider a triangle correspondence △ABC ↔ △XYZ that corresponds to two pairs of equal sides and one pair of equal, non-included angles. If the triangles are not identical, then △ABC can be made to be identical to △XYZ by swinging the appropriate side along the path of a circle with a radius length of that side.
• A triangle drawn under the condition of two sides and a non-included angle, where the angle is 90° or greater, does determine a unique triangle.
Lesson 12 Classwork
Exploratory Challenge
1. Use your tools to draw △ABC, provided AB = 5 cm, BC = 3 cm, and ∠A = 30°. Continue with the rest of the problem as you work on your drawing.
a. What is the relationship between the given parts of △ABC?
b. Which parts of the triangle can be drawn without difficulty? What makes this drawing challenging?
c. A ruler and compass are instrumental in determining where C is located.
• Even though the length of AC is unknown, extend the ray AC in anticipation of the intersection with BC.
• Draw segment BC with length 3 cm away from the drawing of the triangle.
• Adjust your compass to the length of BC.
• Draw a circle with center B and a radius equal to BC, or 3 cm.
d. How many intersections does the circle make with AC? What does each intersection signify?
e. Complete the drawing of △ABC.
f. Did the results of your drawing differ from your prediction?
2. Now attempt to draw this triangle: draw △DEF, provided DE = 5 cm, EF = 3 cm, and ∠F = 90°.
a. How are these conditions different from those in Exercise 1, and do you think the criteria will determine a unique triangle?
b. What is the relationship between the given parts of △DEF?
c. Describe how you will determine the position of DE.
d. How many intersections does the circle make with FE?
e. Complete the drawing of △DEF. How is the outcome of △DEF different from that of △ABC?
f. Did your results differ from your prediction?
3. Now attempt to draw this triangle: draw △JKL, provided KL = 8 cm, KJ = 4 cm, and ∠J = 120°. Use what you drew in Exercises 1 and 2 to complete the full drawing.
4. Review the conditions provided for each of the three triangles in the Exploratory Challenge, and discuss the uniqueness of the resulting drawing in each case.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.