

Construct A Triangle Given Two Sides And An Angle
Related Topics:
More Lessons for Grade 6
Math Worksheets
In this lesson, we will learn how to construct a triangle given two sides and an angle between them (SAS). In order for the triangle to be unique, the angle given must be between the two given sides.
Example:
How to construct a triangle given two sides and the included angle (SAS)?
1. Draw a rough sketch of the construction.
2. Measure and draw out one of the line segments (usually the longer one).
3. Construct the angle from the base, using a protractor.
4. Set compasses to the second given length, position compass point at center of angle and draw an arc that intersects the second line.
5. Connect this intersection with the other end of the base.
Construction: Triangle - 2 Sides, 1 Angle
A demonstration of how to construct a triangle, give the lengths of two sides and the angle between them. How to construct a congruent triangle using the side-angle-side congruence postulate?
How to construct a triangle given two angles and the side in between (ASA)?
1. Draw a rough sketch of the construction.
2. Measure and draw out one of the line segments (usually the longer one).
3. Construct the first angle from one end of the base, using a protractor.
4. Construct the second angle from the other end of the base, using a protractor.
5. The two constructed angles will intersect creating the third vertex.


More Lessons for Grade 6
Math Worksheets
In this lesson, we will learn how to construct a triangle given two sides and an angle between them (SAS). In order for the triangle to be unique, the angle given must be between the two given sides.
Example:
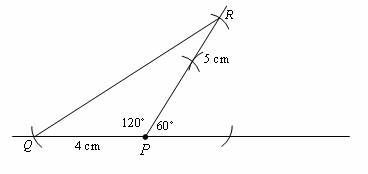
Construct a triangle PQR given that PQ = 4 cm, PR = 5 cm and ![]() = 120˚.
= 120˚.
Solution:
Step 1:
We construct a 60˚ angle and get the supplementary angle, which is 120˚.
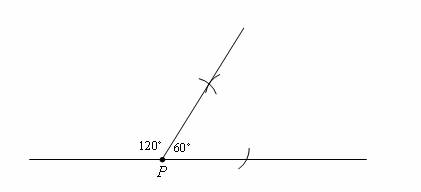
Step 2 :
We construct 2 line segments of 4 cm and 5 cm from P respectively. Then, draw a line from Q to R to form the triangle.
1. Draw a rough sketch of the construction.
2. Measure and draw out one of the line segments (usually the longer one).
3. Construct the angle from the base, using a protractor.
4. Set compasses to the second given length, position compass point at center of angle and draw an arc that intersects the second line.
5. Connect this intersection with the other end of the base.
Construction: Triangle - 2 Sides, 1 Angle
A demonstration of how to construct a triangle, give the lengths of two sides and the angle between them. How to construct a congruent triangle using the side-angle-side congruence postulate?
How to construct a triangle given two angles and the side in between (ASA)?
1. Draw a rough sketch of the construction.
2. Measure and draw out one of the line segments (usually the longer one).
3. Construct the first angle from one end of the base, using a protractor.
4. Construct the second angle from the other end of the base, using a protractor.
5. The two constructed angles will intersect creating the third vertex.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.