

Properties of the Angles Of A Triangle
More Geometry Lessons
Geometry Worksheets
Geometry Games
In these lessons, we will give a summary of the properties of the angles of a triangle.
- Triangle Sum Theorem - The sum of the 3 angles in a triangle is always 180°
- The sum of an interior angle and its adjacent exterior angle is 180°
- Exterior Angle Theorem - An exterior angle of a triangle is equal to the sum of the two opposite interior angles
- An equilateral triangle has 3 equal angles that are 60° each. An isosceles triangle has 2 equal angles, which are the angles opposite the 2 equal sides
The angles of a triangle have the following properties:
Property 1: Triangle Sum Theorem
The sum of the 3 angles in a triangle is always 180°.Example :
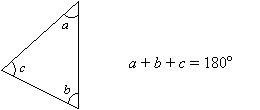
How to prove the Triangle Sum Theorem?
The following video shows how to prove that the sum of the angles of a triangle is 180 degrees. (Triangle Sum Theorem)
How to Find the Missing Angle in a Triangle Using the Triangle Sum Theorem?
Step 1: Write out the equation by adding all the angles and making them equal to 180°.
Step 2: Solve for x.
Step 3: Substitute to find the missing angles.
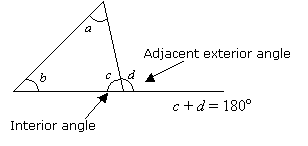
Property 2:
The sum of an interior angle and its adjacent exterior angle is 180°.Example :
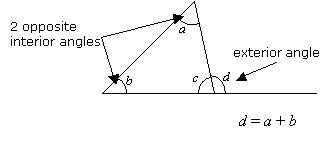
Property 3: Exterior Angle Theorem
An exterior angle of a triangle is equal to the sum of the two opposite interior angles.Example :
Finding the Unknown Angle of a Triangle
Example:
1. Evaluate triangle abc, where a = 40° and b = 60°. What is the exterior angle to ∠acb?
2. Evaluate triangle abc, where a = 50° and b = 30°. What is the exterior angle to ∠acb?
2. Evaluate triangle abc, where a = 90° and b = 40°. What is the exterior angle to ∠acb?
How to use the Exterior Angle Theorem to solve problems involving angles in a triangle?
Property 4:
An equilateral triangle has 3 equal angles that are 60° each.An isosceles triangle has 2 equal angles, which are the angles opposite the 2 equal sides.
How to Find the Missing Angle in an Isosceles Triangle? Parallel Lines and the Triangle Angle-Sum Theorem
The above angle properties can help us to find unknown angles in a triangle.
Example:
Find the value of x in the following triangle.
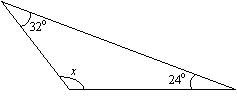
Solution:
x + 24° + 32° = 180° (sum of angles is 180°)
x + 56° = 180°
x = 180° – 56° = 124°
Example :
Find the values of x and y in the following triangle.
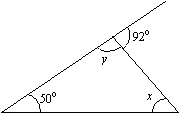
Solution:
x + 50° = 92° (sum of opposite interior angles = exterior angle)
x = 92° – 50° = 42°
y + 92° = 180° (interior angle + adjacent exterior angle = 180°.)
y = 180° – 92° = 88°
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.