Surface Area of a Sphere
In these lessons we will learn
- the formula of the surface area of a sphere.
- how to calculate the surface area of a sphere.
- how to calculate the surface area of a hemisphere.
- how to solve problems about the surface area of spheres.
- how to prove the formula of the surface area of a sphere.
Related Pages
Surface Area Of Spheres Worksheet
More Geometry Lessons
Surface Area of a Sphere
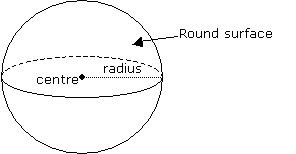
A sphere is a solid in which all the points on the round surface are equidistant from a fixed point, known as the center of the sphere. The distance from the center to the surface is the radius.
Surface area of a sphere is given by the formula:
Surface Area of sphere = 4πr2
where r is the radius of the sphere.
Example:
Calculate the surface area of a sphere with radius 3.2 cm
Solution:
Surface area of sphere
= 4π r2
= 4π (3.2)2
= 4 × 3.14 × 3.2 × 3.2
= 128.6 cm2
Worksheetto calculate the surface area of spheres.
How to find the surface area of a sphere?
Example:
Find the surface area of a sphere with r = 4 ft
How to calculate the surface area of a sphere given the radius or diameter?
Example:
Find the surface area of a sphere with diameter = 22 cm
Surface Area of a hemisphere
A hemisphere is half a sphere, with one flat circular face and one bowl-shaped face.
The surface area of a hemisphere is equal to the area of the curve surface plus the area of the circular base.
Surface area of hemisphere
= 
× surface area of sphere + area of base
= × 4π r2 + π r2 = 3π r2
Example:
Calculate the surface area of a hemisphere with radius 4 cm
Solution:
Surface area of hemisphere
= × surface area of sphere + area of base
= × 4π r2 + π r2
= 3π r2
= 3π (4)2
= 150.86 cm2
Problems about surface area of spheres
Problem: What is the radius of the sphere given the surface area?
Example: What is the radius of a sphere with a surface area of 900π?
Problem:
The surface area of a sphere is 5024 square meters. What is the volume of the sphere? Use 3.14 for pi. Round your answer to the nearest cubic meter.
Problem:
The radius of a sphere is tripled.
a) Describe the effect on the volume.
b) Describe the effect on the surface area.
Proof of the formula of the surface area of a sphere
This video demonstrates that the surface area of a sphere equals the area of 4 circles. (It is not a formal proof)
The formula for the surface of a sphere is derived by summing up small ring elements of area along its perimeter. (uses calculus)
These two videos explain the Archimedes method of deriving the surface area of a sphere.
Part1:
Part 2:
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.