

Rational and Irrational Numbers
Common Core (The Real Number System)
Common Core for Mathematics
Examples, solutions, videos, and lessons to help High School students explain why the sum or product of two rational numbers is rational; that the sum of a rational number and an irrational number is irrational; and that the product of a non-zero rational number and an irrational number is irrational.
- Simplify radical expressions.
- Add, subtract, and multiply real numbers.
- Explain why adding and multiplying two rational numbers results in a rational number.
- Explain why adding a rational number to an irrational number results in an irrational number.
- Explain why multiplying a nonzero number to an irrational number results in an irrational number.
Rational + Rational = Rational
Rational + Irrational = Irrational
Irrational + Irrational = Can be Rational or Irrational
Rational × Rational = Rational
Rational × Irrational = Irrational
Irrational × Irrational = Can be Rational or Irrational
Common Core: HSN-RN.B.3
The following diagram shows the sum and product of rational and irrational numbers. Scroll down the page for proofs, examples, and solutions on using the sum and product of rational and irrational numbers.
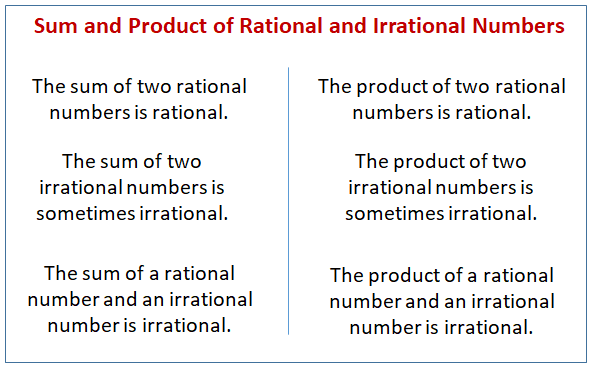
Learn that the sum or the product of two rational numbers is always a rational number.
Rational + Rational = Rational
Rational × Rational = Rational
Sums and products of irrational numbers
Sums and products of irrational numbers maybe rational or irrational.
Irrational + Irrational = Can be Rational or Irrational
Irrational × Irrational = Can be Rational or Irrational
Rational + Irrational = Irrational
Proof that rational times irrational is irrational
Rational × Irrational = Irrational
Rational vs. Irrational Numbers
This video explains the difference between rational and irrational numbers and how to identify rational and irrational numbers. Irrational Numbers
Although the Greeks initially thought all numeric qualities could be represented by the ratio of two integers, i.e. rational numbers, we now know that not all numbers are rational. How do we know this. Adding Rational and Irrational Numbers
Rational + Rational = Rational
Rational + Irrational = Irrational. Product & quotient of 2 rationals, 2 irrationals or 1 of each
Rational × Rational = Rational
Rational × Irrational = Irrational
Irrational × Irrational = Rational or Irrational
Rational ÷ Rational = Rational
Rational ÷ Irrational = Irrational
Irrational ÷ Irrational = Rational or Irrational Sums and products of rationals and irrationals - Song
This is a song that teaches about adding and multiplying rational numbers and irrational numbers. The song lines up with the following high school common core standard : CCSS.Math.Content.HSN-RN.B.3
Rational + Rational = Rational
Rational + Irrational = Irrational
Rational × Rational = Rational
Rational × Irrational = Irrational
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.