Pythagorean Triples
In these lessons, we will learn
- Pythagorean Triples
- families of Pythagorean Triples
- Pythagorean Triples and right triangles
- solving problems using the Pythagorean Triples
- how to generate Pythagorean Triples
Related Pages
Pythagorean Theorem
Converse Of Pythagorean Theorem
Pythagorean Theorem Word Problems
Applications Of Pythagorean Theorem
More Geometry Lessons
Pythagorean Triples
Pythagorean triples are formed by positive integers a, b and c, such that a2 + b2 = c2. We may write the triple as (a, b, c).
For example, the numbers 3, 4 and 5 form a Pythagorean Triple because 32 + 42 = 52. There are infinitely many Pythagorean triples.
Some examples are:
| ( 3 , 4 , 5 ) | ( 5, 12, 13) | ( 7, 24, 25) | ( 8, 15, 17) |
| ( 9, 40, 41) | (11, 60, 61) | (12, 35, 37) | (13, 84, 85) |
| (16, 63, 65) | (20, 21, 29) | (28, 45, 53) | (33, 56, 65) |
| (36, 77, 85) | (39, 80, 89) | (48, 55, 73) | (65, 72, 97) |
Families of Pythagorean Triples
If we multiply each number of a Pythagorean triple by the same number, we form another Pythagorean triple.
For example, (6, 8, 10) is a family of the Pythagorean triple (3, 4, 5) because it can be obtained by 2 × 3 = 6, 2 × 4 = 8, 2 × 5 = 10. If we multiply (3, 4, 5) by 3, we get another triple (9, 12, 15). This can be repeated with different multiples.
Similarly, the family for (5, 12, 13) would be (10, 24, 26), (15, 36, 39) and so on.

Pythagorean Triples and Right Triangles
When we make a triangle with sides whose lengths are the Pythagorean Triples, the triangle will form a right triangle. This follows from the converse of the Pythagorean Theorem.
The following diagram shows some examples of Pythagorean Triples. Scroll down the page for more examples and solutions on Pythagorean Triples and Right Triangles.

Memorizing some common Pythagorean triples can helpful.
For example, if we see that the sides of a triangle form a Pythagorean triple then we know that it is a right triangle.
The following video gives some examples of Pythagorean triples and right triangles.
Any group of 3 integer values that satisfies the equation a2 + b2 = c2 is
called a Pythagorean Triple. Therefore, any triangle that has sides that form a Pythagorean Triple must be
a right triangle.
Solving Problems Using The Pythagorean Triples
Pythagorean triples may also help us to find the missing side of a right triangle faster. If two sides of a right triangle form part of a triple then we can know the value of the third side without having to calculate using the Pythagorean theorem.
Example:
Find the value of x
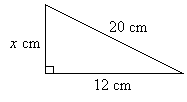
Solution:
Check for Pythagorean triple:
Get the ratio of the two given sides:
12 : 20 = 3 : 5 ( divide by 4 )
From the ratio, we know that it is a Pythagorean triple.
So, x = 4 × 4 = 16 cm
The following videos show how to solve some GMAT, SAT and ACT questions using the Pythagorean Triples
How To Generate Pythagorean Triples
The following video will show you how to use an ordinary multiplication table to list infinitely many different examples of Pythagorean Triples.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.