

Math - Grade 6 (Number Relationships)
More Lessons for Grade 6 Math
Grade 6 Worksheets
Number Worksheets
Number Games
In these lessons, we will learn how to find the factors and multiples of a number.
We will visualize factors using Arrays, Factor Lists and Factor Rainbows.
We will learn what are the multiples of a number.
We will learn how to differentiate between Prime Numbers and Composite Numbers.
We will learn a technique called "The Sieve of Eratosthenes" to find prime numbers.
We will learn how to perform Prime Factorization using Factor Trees and Repeated Division. Factors
Factors are numbers that when multiplied, produce a product. Factors always come in pairs.
For example, the factors of 12 are 1 and 12, 2 and 6, 3 and 4.
There are severals ways that we can use to help us visualize and find the factors of a number.
We can use arrays to represent factors.
The ways we can arrange 12 tiles to make complete rectangles represent the factors of 12.

We can create an organized list of the factors of a given number. We identify the number and then list the factors in a row. When listing the factors of a number, start on the left and list them in ascending order to ensure that you do not omit any.

Another visual representation that we can use to help factor numbers is the factor rainbow. In a factor rainbow, we begin listing the factors of the number, horizontally, starting at 1. When the factor pairs are connected curved lines create a rainbow shape.
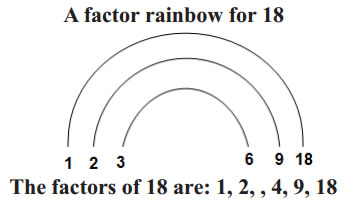
In this lesson, we will learn how to write down the factors of a number.
First, we discuss what a factor is and why it is important. Then we work several examples of finding factors of numbers. Finding factors is important when working with fractions learning how to simplify fractions. Finding Factors Using Factor Rainbow Multiples
When we multiply two factors, the product is a multiple of those two factors.
E.g., 2 × 5 = 10. 2 and 5 are the factors of 10, whereas 10 is a multiple of 2 and 5.
Note that 0 as a multiple of any number.
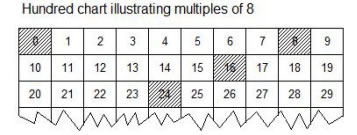
We can identify the multiples of a number using a hundred chart.
We can start at 0 and then skip count the specified number. For example, to find the multiples of 8, we can start at 0, and shade in every 8 numbers. The shaded numbers are the multiples of 8. Don't forget to include 0.
We can use a number line to skip count by the specified number.

We can use an organized chart to identify multiples of a number. Here, we use the multiplication of the number 8 by various factors to determine multiples of 8.

Factors and Multiples
This video shows you the difference between factors and multiples and how to find them using any number.
Prime and Composite Numbers
A prime number is a number whose only factors are 1 and itself. For example, 2, 3, 5, 7, 11, 13, 17 etc.
A composite number is a number that has more than two factors. For esample, 4, 6, 8, 9, 10, 12, 14 etc.
The number 1 is neither prime nor composite because it has only one factor.
0 is another special number. 0 cannot be a prime number because every number is a factor of zero. 0 x 1 does equal 0, but 0 multiplied by anything equals 0.
0 is not a composite number because it cannot be written as a product of two factors, neither of which is itself.
One way to visualize prime and composite numbers is to use arrays. Numbers that can only be arranged in one array are prime numbers. Numbers that can be arranged in more than one array are composite.
Prime and composite numbers Prime and Composite Numbers
Check whether a number is prime or composite using factor rainbows. An interesting way to help students determine whether a number is prime or composite is a technique called "The Sieve of Eratosthenes".
Use a hundred chart to find the primes from 1-100:
Step 1: Cross out 1 because 1 is not a prime.
Step 2: Circle 2 and cross out all multiples of 2. (2, 4, 6, 8, 10, ...)
Step 3: Circle 3 and cross out all multiples of 3. (3, 6, 9, 12, 15, ...)
Step 4: Circle 5 and cross out all multiples of 5. (5, 10, 15, 20, ...)
Step 5: Circle 7 and cross out all multiples of 7. (7, 14, 21, 28, ...)
Circle all the numbers that are not crossed out and they are the prime numbers less than 100.
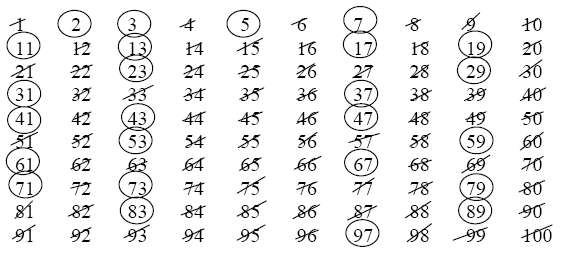
Sieve of Eratosthenes explained (Prime Numbers, Factors, Multiples)
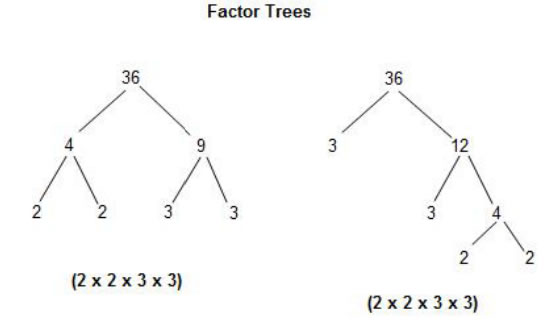
Prime Factorization
Any one number can be broken
down into a series of prime numbers. This is called prime factorization.
E.g. 24 = 2 × 12 = 2 × 2 × 6 = 2 × 2 × 2 × 3
We can use Factor Trees
to help us find the prime factors of a number. Note that regardless of where you start the factorization process, you will always end with the same
prime factors.
We can also use repeated division to find the prime factors of a numbers.

Prime Factorization
Prime factorization is the process of decomposing a number to only its prime factors.
This video shows how to perform prime factorization using factor trees and repeated division.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.