

Functions
A function indicates the relationship between variables. If y is a function of x, the value of y depends on the value of x and for each value of x there is only one value of y.
In other words, think of a function as a rule of correspondence assigning a single value of y to every value of x.
Notation Of Functions
The equation y = x + 3 can also be thought of as a function, where the value of y depends on the value of x. Each value of x yields only one value of y.
We write the function as: f(x) = x + 3
In function notation, y is replaced by f(x).
f (x) is used to denote a function of x and it is read as ‘ f of x’.
f(x) is also called the function value of x under f.
The letter x stands for the variable of f.
When the variable x is given a value, f(x) will then have a value. For example, f(1) is the function value under f when x takes on the value 1.
Example:
Given f(x) = x2 + 2x, find the value of f(3)
Solution:
f(3) = (3)2 + 2(3) = 9 + 6 = 15
Composite Functions
A composite function is a composition of 2 or more functions into a single function.
Let us look at a composite function pictorially. Suppose f and g are 2 functions. The diagram below describes what the composite function gf is.
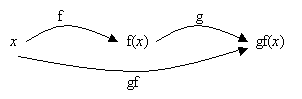
The 2 short arrows represent f and g respectively. First f maps value x to function value f(x). Then g maps value f(x) to function value g(f(x)). In this case, the function value f(x) becomes the input for the variable in g(x) for the second arrow. The resulting value under function g is g(f(x)).
The long arrow represents gf as a single function. This function maps x directly to the function value g(f(x)).
In other words, the long arrow produces the same result as the end result of the 2 short arrows in 2 “hops”. gf is called the composite function of f and g.
Example:
Given f (x) = 2x + 1 and g(x) = x2 – 2, find: gf (5)
Solution:
gf (5) = g( f(5))
= g(2(5) + 1)
= g(11)
= 112 – 2
= 119
Examples of functions and composite functions.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.