

Isosceles Triangle Theorem
Related Topics:
More Lessons for Grade 9
Math Worksheets
Examples, solutions, videos, worksheets, games, and activities to help Geometry students learn about the isosceles triangle theorem.
What are the Isosceles Triangle Theorems?
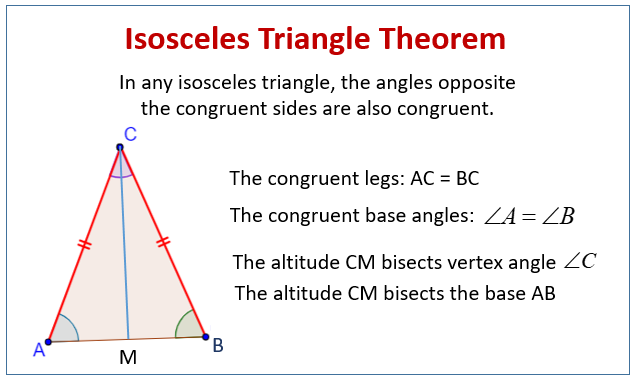
1. If two sides of a triangle are congruent, the angles opposite them are congruent.
2. If two angles of a triangle are congruent, the sides opposite them are congruent.
3. The altitude to the base of an isosceles triangle bisects the vertex angle.
4. The altitude to the base of an isosceles triangle bisects the base.
The following diagram shows the Isosceles Triangle Theorem. Scroll down the page for more examples and solutions on the Isosceles Triangle Theorem.
Isosceles triangles have at least two congruent sides and at least two congruent angles. The congruent sides, called legs, form the vertex angle. The other two congruent angles are the base angles. Isosceles triangles are used in the regular polygon area formula and isosceles right triangles are known as 45-45-90 triangles.
Isosceles Triangle Theorem
How to use the Isosceles Triangle Theorem to find missing sides or missing angles? The Isosceles Triangle Theorem
Students learn that an isosceles triangle is composed of a base, two congruent legs, two congruent base angles, and a vertex angle. Students also learn the isosceles triangle theorem, which states that if two sides of a triangle are congruent, then the angles opposite those sides are congruent; and the converse of the isosceles triangle theorem, which states that if two angles of a triangle are congruent, then the sides opposite those angles are congruent. Students are then asked to solve problems related to these theorems using Algebra. Isosceles triangles 1 Isosceles triangles 2


More Lessons for Grade 9
Math Worksheets
Examples, solutions, videos, worksheets, games, and activities to help Geometry students learn about the isosceles triangle theorem.
What are the Isosceles Triangle Theorems?
1. If two sides of a triangle are congruent, the angles opposite them are congruent.
2. If two angles of a triangle are congruent, the sides opposite them are congruent.
3. The altitude to the base of an isosceles triangle bisects the vertex angle.
4. The altitude to the base of an isosceles triangle bisects the base.
The following diagram shows the Isosceles Triangle Theorem. Scroll down the page for more examples and solutions on the Isosceles Triangle Theorem.
Isosceles triangles have at least two congruent sides and at least two congruent angles. The congruent sides, called legs, form the vertex angle. The other two congruent angles are the base angles. Isosceles triangles are used in the regular polygon area formula and isosceles right triangles are known as 45-45-90 triangles.
How to use the Isosceles Triangle Theorem to find missing sides or missing angles? The Isosceles Triangle Theorem
Students learn that an isosceles triangle is composed of a base, two congruent legs, two congruent base angles, and a vertex angle. Students also learn the isosceles triangle theorem, which states that if two sides of a triangle are congruent, then the angles opposite those sides are congruent; and the converse of the isosceles triangle theorem, which states that if two angles of a triangle are congruent, then the sides opposite those angles are congruent. Students are then asked to solve problems related to these theorems using Algebra. Isosceles triangles 1 Isosceles triangles 2
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.