Sets Intersection: Intersection Of Three Sets
In these lessons, we will learn the intersection of three sets, how to shade regions of Venn Diagrams involving three sets and how to solve problems using the Venn Diagram of three sets (three circles).
Related Pages
Intersection Of Two Sets
Venn Diagrams
More Lessons On Sets
Venn Diagrams Of Three Sets
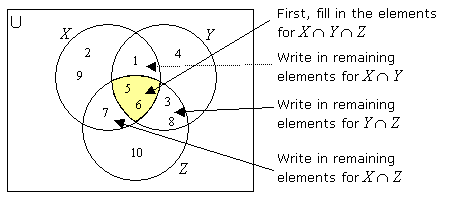
The intersection of three sets X, Y and Z is the set of elements that are common to sets X, Y and Z. It is denoted by X ∩ Y ∩ Z.
Example:
Draw a Venn diagram to represent the relationship between the sets
X = {1, 2, 5, 6, 7, 9}, Y = {1, 3, 4, 5, 6, 8} and
Z = {3, 5, 6, 7, 8, 10}
Solution:
We find that X ∩ Y ∩ Z = {5, 6}, X ∩ Y = {1, 5, 6},
Y ∩ Z = {3, 5, 6, 8} and X ∩ Z = {5, 6, 7}
For the Venn diagram:
Step 1: Draw three overlapping circles to represent the three sets.
Step 2: Write down the elements in the intersection X ∩ Y ∩ Z.
Step 3: Write down the remaining elements in the intersections:
X ∩ Y, Y ∩ Z and X ∩ Z.
Step 4: Write down the remaining elements in the respective sets.
Notice that you start filling the Venn diagram from the elements in the intersection first.
In general, there are many ways that 3 sets may intersect. Some examples are shown below.
How To Shade Regions Of Venn Diagrams Involving Three Sets
Venn Diagrams: Shading Regions with Three Sets, Part 1 of 2
This video shows how to shade regions of Venn Diagrams involving three sets.
Example:
Shade the indicated region:
- (A ∩ B) ∩ C
- (A ∪ B) ∩ C
Venn Diagrams: Shading Regions with Three Sets, Part 2 of 2
More example to show to shade regions of Venn Diagrams involving three sets.
Example:
Shade the indicated region:
3) (A ∪ B)' ∩ C
4) (A' ∩ B') ∩ C'
How To Write An Expression For A Venn Diagram Region?
Create an expression to represent the outlines part of the Venn Diagram shown.
How To Solve Word Problems With 3-Set Venn Diagrams?
Venn Diagram Problem With 3 Circles
Use the given information to fill in the number of elements in each region of the Venn Diagram.
This video solves two problems using Venn Diagrams. One with two sets and one with three sets.
Example 1:
150 college freshmen were interviewed.
85 were registered for a math class
70 were registered for an English class
50 were registered for both math and English
- How many signed up only for a math class?
- How many signed up only for an English class?
- How many signed up for math or English?
- How many signed up for neither math nor English?
Example 2:
100 were students interviewed
28 took PE
31 took Bio
42 took Eng
9 took PE and Bio
10 took PE and Eng
6 took Bio and Eng
4 took all three subjects
How many students took none of the three subjects?
How many students took PE, but not Bio or Eng?
How many students took Gio and PE but not Eng?
How To Solve A Venn Diagram Problem Involving Three Sets?
Example:
110 college freshmen were surveyed
25 took physics
45 took biology
45 took mathematics
10 took physics and mathematics
8 took biology and mathematics
6 took physics and biology
5 took all three
a. How many students took biology, but neither physics nor mathematics?
b. How many students took biology, physics or mathematics?
c. How many students did not take any of the three subjects?
How to fill up a 3-circle Venn Diagram?
In this video we go over a basic word problem involving three sets. We use a Venn diagram to
answer the series of questions.
Venn Diagram Shading Calculator Or Solver
Enter an expression like (A Union B) Intersect (Complement C) to describe a combination of two or three
sets and get the notation and Venn diagram. Use parentheses, Union, Intersection, and Complement.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.