

Increase Exponentially
Videos and lessons with examples and solutions to help High School students observe using graphs and tables that a quantity increasing exponentially eventually exceeds a quantity increasing linearly, quadratically, or (more generally) as a polynomial function.
Related Topics:Common Core (Functions)
Common Core Mathematics
The following graphs compare an exponential function, a quadratic function and a linear function. Scroll down the page for more examples and solutions.
Exponential growth always surpasses linear, quadratic, and cubic growth.
Examples:
1. Given the functions f(x) = 3x + 7 and g(x) = (7/4)x - 3, where x ≥ 2. Which point is closest to where g(x) begins to exceed f(x)?
A. x = 7
B. x = 6
C. x = 4
D. x = 9
2. Values for the function are shown in the table. Which statement proves that it is an exponential function>
A. All of the values are odd numbers.
B. All of the values are multiples of 3.
C. The function grows by equal factors over equal intervals.
D. The function grows by equal differences over equal intervals.
Comparing and contrasting Exponential and Linear Functions
Examples:
1. Compare f(x) = 2 • 3x and g(x) = 3x = 2
2. Compare f(x) 6 • (1/3)x and g(x)
3. What type of function best describes the following situations? Explain your answers.
a. Marcus invests $1000 into a bank account that earns 3% interest annually. He has not taken out any money or added any money to his account since he appointed the original $1000.
b. Ginny has $1000 that she keeps in her piggy bank at home. She never spends any of this money but she does add $50 to her piggy bank every year.
c. Will Ginny always have more money than Marcus? Comparing growth of exponential & quadratic models
This video discusses two functions that model the shipment rate of cars. One function is quadratic and the other is exponential. Which one will eventually exceed the other?
Example:
The Cozy Car Company ships some of their new cars to Japan and Vietnam. The number of cars that will be shipped to Japan during the next t months is modeled by the function f(t) = 2t. The number of cars that will be shipped to Vietnam during the next t months is modeled by the function f(t) = 2t2
a) Which country had received more cars from the Cozy Car Company after 5 months?
b) Which country had received more cars from the Cozy Car Company after 7 months?
c) Will the country which received more cars from Cozy Car company after 7 monthe continue to receive more cars than the other country in future months?


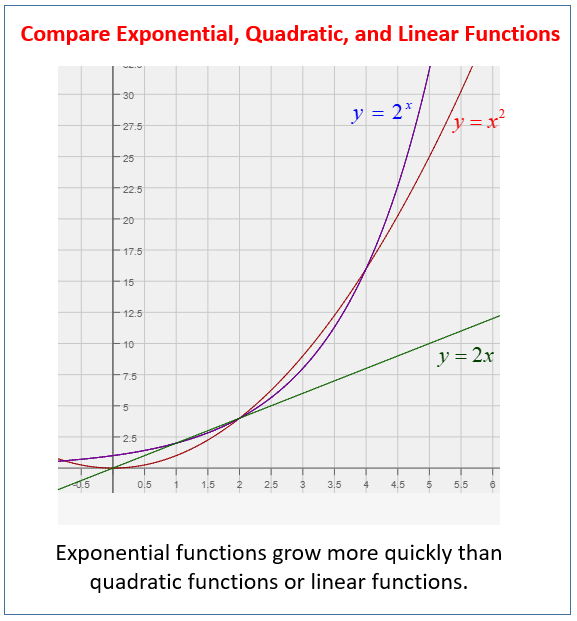
- Use a table to observe that exponential functions grow more quickly than quadratic functions.
- Use a graph to observe that exponential functions grow more quickly than quadratic functions.
Common Core: HSF-LE.A.3
Compare polynomial and exponential growth - F-LE.3Exponential growth always surpasses linear, quadratic, and cubic growth.
Examples:
1. Given the functions f(x) = 3x + 7 and g(x) = (7/4)x - 3, where x ≥ 2. Which point is closest to where g(x) begins to exceed f(x)?
A. x = 7
B. x = 6
C. x = 4
D. x = 9
2. Values for the function are shown in the table. Which statement proves that it is an exponential function>
A. All of the values are odd numbers.
B. All of the values are multiples of 3.
C. The function grows by equal factors over equal intervals.
D. The function grows by equal differences over equal intervals.
Examples:
1. Compare f(x) = 2 • 3x and g(x) = 3x = 2
2. Compare f(x) 6 • (1/3)x and g(x)
3. What type of function best describes the following situations? Explain your answers.
a. Marcus invests $1000 into a bank account that earns 3% interest annually. He has not taken out any money or added any money to his account since he appointed the original $1000.
b. Ginny has $1000 that she keeps in her piggy bank at home. She never spends any of this money but she does add $50 to her piggy bank every year.
c. Will Ginny always have more money than Marcus? Comparing growth of exponential & quadratic models
This video discusses two functions that model the shipment rate of cars. One function is quadratic and the other is exponential. Which one will eventually exceed the other?
Example:
The Cozy Car Company ships some of their new cars to Japan and Vietnam. The number of cars that will be shipped to Japan during the next t months is modeled by the function f(t) = 2t. The number of cars that will be shipped to Vietnam during the next t months is modeled by the function f(t) = 2t2
a) Which country had received more cars from the Cozy Car Company after 5 months?
b) Which country had received more cars from the Cozy Car Company after 7 months?
c) Will the country which received more cars from Cozy Car company after 7 monthe continue to receive more cars than the other country in future months?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.