Implicit Differentiation

In this lesson, we will learn how implicit differentiation can be used the find the derivatives of equations that are not functions.
Related Topics: More Lessons on Calculus

Some functions can be described by expressing one variable explicitly in terms of another variable.

For example:
y = x² + 3
y = x cos x

However, some equations are defined implicitly by a relation between x and y.

For example:
x² + y² = 16
x² + y² = 4xy

We do not need to solve an equation for y in terms of x in order to find the derivative of y. Instead, we can use the method of implicit differentiation. This involves differentiating both sides of the equation with respect to x and then solving the resulting equation for y’.

A set is a collection of objects, things or symbols which are clearly defined.
The individual objects in a set are called the members or elements of the set.
A set must be properly defined so that we can find out whether an object is a member of the set.

1. Listing the elements (Listing Method)

The set can be defined by listing all its elements, separated by commas and enclosed within braces. This is called the roster method.

Example:
B = {2, 4, 6, 8, 10}
X = {a, b, c, d, e}

However, in some instances, it may not be possible to list all the elements of a set. In such cases, we could define the set by method 2.

Example:

If x² + y² = 16, find

Solution:

Step 1: Differentiate both sides of the equation

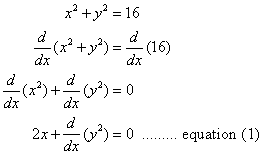
Step 2: Using the Chain Rule, we find that

Step 3: Substitute equation (2) into equation (1)

Step 4: Solve for

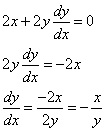
Example:

Find y’ if x³ + y³ = 6xy

Solution:

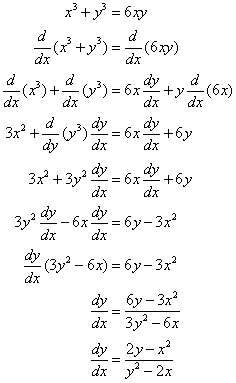
Videos

Implicit Differentiation - Basic Idea and Examples
The basic idea about using implicit differentiation

More! Implicit Differentiation Examples

More Implicit Differentiation Examples - 3

Using Implicit Differentiation to Find a Derivative Using Implicit Differentiation to Find a Derivative