Geometry and Probability
Related Topics: More Probability Lessons
In these lessons, we will learn how to solve probability problems that may involve geometry and the area of geometrical shapes.
Example:
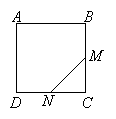
ABCD is a square. M is the midpoint of BC and N is the midpoint of CD. A point is selected at random in the square. Calculate the probability that it lies in the triangle MCN.
Solution:
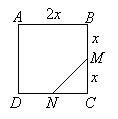
Let 2x be the length of the square.
Area of square = 2x × 2x = 4x2
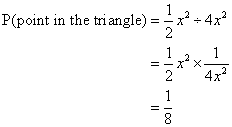
Example:
The figure shows a circle with centre O and radius 8 cm. Ð* BOD* = 72˚. The radius of the smaller circle is 4 cm. A point is selected at random inside the larger circle BCDE.
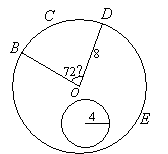
Calculate the probability that the point lies
a) inside the sector BODC.
b) inside the smaller circle
c) neither in the sector BODC nor in the smaller circle.
Solution:
a) ![]()
Area of sector BODC = ![]() × area of the large circle
× area of the large circle
Probability that the point lies in sector BODC = ![]()
b) ![]()
Area of smaller circle = ![]() × area of the large circle
× area of the large circle
Probability that the point lies in the smaller circle = ![]()
c) Probability that the point does not lie in sector BODC or the smaller circle
Geometric Probability with Area
Example 1:
A circle with radius 2 lies inside a square with side length 6. A dart lands randomly inside the square. What is the probability the dart lands inside the circle? Give the exact probability and the probability as a percent rounded to the nearest tenth.
Example 2:
A point is chosen at random on the given figure. What is the probability that the point is in the yellow region?
Example 3:
A square is inscribed in a circle. What is the probability that a point chosen inside the circle will be inside the square?
Example 4:
A circle is inscribed in a equilateral triangle. What is the probability that a point chosen at random inside the triangle will be insode the circle?
Using Area to find Probability
Example:
A circle is inscribed in a square. Point Q in the square is chosen at random. What is the probability that Q lies in the shaded region?
Geometric Probability and Areas of Sectors
Geometric Probability is probability that involves geometric measures (typically length or area)
Example:
Find the area of the indicated sector. Then find the probability of spinning the color indicated if the diameter is 12 cm.
Study Guide Area Probability Problem 1
Example:
Find the probability that a point randomly selected from the figure will land in the shaded area.
Study Guide Area Probability Problem 2
Example:
Find the probability that a point randomly selected from the figure will land in the shaded area.
Geometric Probability
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.