SAT Practice Test 8, Section 8: Questions 11 - 16

Related Topics:
More Lessons for SAT Preparation

Math Worksheets

This is for SAT in Jan 2016 or before.

The following are worked solutions for the questions in the math sections of the SAT Practice Tests found in the The Official SAT Study Guide Second Edition.

It would be best that you go through the SAT practice test questions in the Study Guide first and then look at the worked solutions for the questions that you might need assistance in. Due to copyright issues, we are not able to reproduce the questions, but we hope that the worked solutions will be helpful.

11. Correct answer: (A)

Given:
x and y are positive integers

To find:
x in terms of y

Solution:
Topic(s): Exponents

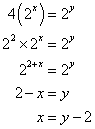
Answer: (A) y – 2

12. Correct answer: (C)

Given:
The degree measures of the angles of a triangle are in the ratio 2:3:4

To find:
How many degrees the measure of the largest angle exceed the measure of the smallest angle

Solution:
Topic(s): Ratio, sum of angles in a triangle

The ratio of the angles is 2:3:4

2x + 3x + 4x = 180 (sum of angles in a triangle = 180)
9x = 180
x = 20

Difference between largest angle and smallest angle is 4x – 2x = 2x
2x = 2 × 20 = 40

Answer: (C) 40

13. Correct answer: (D)

Given:
The rate of telephone call is 50 cents for the 1 st minute and 30 cents for each additional minute or portion thereof

To find:
The function that describes the cost, in dollars, of a phone call that lasts for n minutes, where n is a positive integer

Solution:
If the phone call last n minutes then the first minute costs $0.50 and the next n – 1 minutes costs (n – 1)$0.30

f(n) = 0.50 + 0.30(n – 1)

Answer: (D) f(n) = 0.50 + 0.30(n – 1)

14. Correct answer: (E)

Given:
The figure

To find:
z in terms of x and y

Solution:
Topic(s): Vertical angles, corresponding angles

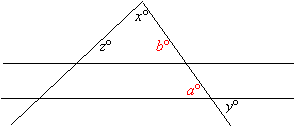
a = y (vertical angle) and b = a (corresponding angle). This implies b = y

x + y + z = 180
z = 180 – x –y

Answer: (E) 180 – x – y

15. Correct answer: (C)

Given:

n and k are positive integers

To find:
The value of k

Solution:

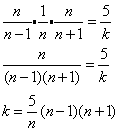
If k is a positive integer then it cannot be 0. So, n cannot be 1.

If n is a positive integer greater than 1 then n – 1 and n + 1 would be positive integers.

In order for k to be a positive integer, must be a positive integer.

The factors of 5 are 1 and 5. Since n cannot be 1, it implies that n = 5

Substituting n = 5 into the above equation

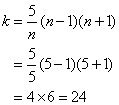
Answer: (C) 24

16. Correct answer: (E)

Given:
m coworkers agree to contribute equally to a lunch that costs a total of y dollars
p of the coworkers fail to contribute

To find:
The expression that represents the additional amount, in dollars, that each of the remaining coworkers must contribute to pay for the lunch

Solution:
If every pays then each worker would need to contribute

If p workers did not pay, the remaining workers must then pay

The additional amount to pay would be

Answer: (E)