SAT Practice Test 3, Section 2: Questions 16 - 20

This is for SAT in Jan 2016 or before.

The following are worked solutions for the questions in the math sections of the SAT Practice Tests found in the The Official SAT Study Guide Second Edition.

It would be best that you go through the SAT practice test questions in the Study Guide first and then look at the worked solutions for the questions that you might need assistance in. Due to copyright issues, we are not able to reproduce the questions, but we hope that the worked solutions will be helpful.

16. Correct answer: (E)

Given:
x and y are consecutive odd integers
y > x

To find:
y² – x²

Solution:
Topic(s): Consecutive numbers, distributive property

Since x and y are consecutive odd integers, we know that y = x + 2.

Substitute y = x + 2 in y 2 – x 2

(x + 2)² – x² = x² + 4x + 4 – x² (use distributive rule)
= 4x + 4

Answer: (E) 4x + 4

17. Correct answer: (A)

Given:
Line l passes through the origin and is perpendicular to the line 4x + y = k , where k is a constant
The two lines intersect at the point (t, t + 1)

To find:
The value of t

Solution:
Topic(s): Equation of a line

Rewrite the equation as y = mx + c, in order to get the slope m.

4x + y = k ⇒ y = 4x + k

The slope is – 4.

In the coordinate plane, two lines are perpendicular if the product of their slopes ( m) is –1.

Let the slope of line l be n. Since line l is perpendicular to the above line:

Line l passes through the origin; this means that its intercept at the y-axis is 0.

The equation for line l is then

(equation 1)

The line l passes through the point (t, t + 1).

Substitute x = t and y = t + 1 into equation 1

Answer: (A)

18. Correct answer: (A)

Given:
Average of x and y is k

To find:
Average of x, y and z

Solution:
Topic(s): Statistics

Given that the average of x and y is k.

Find the average of x, y and z

Answer: (A)

19. Correct answer: (C)

Given:
Given figure
Triangle ABC is equilateral with sides = 2
WY is diameter of circle with center O

To find:
Area of circle

Solution:
Topic(s): Triangles, Pythagoras theorem, area of circle

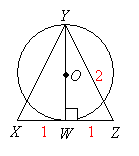
Triangle XYZ is equilateral, with side 2.

Let d = length of YW

Using Pythagorean theorem:

d is also the diameter of the circle.

The radius of the circle is

Area of circle:

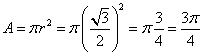
Answer: (C)

20. Correct answer: (C)

Given:
When 15 is divided by the positive integer k, the remainder is 3

To find:
The number of different values of k

Solution:
When 15 is divided by the positive integer k, the remainder is 3 can be translated into the following equation.

15 = nk + 3, where n is a positive integer less than 3

⇒ nk = 12

We now put in the values for n to test how many of them are divisible by 12. (Remember n is positive and less than 3).

n = 1, k = 12

n = 2, k = 6

n = 3, k = 4

There are three possible values for k.

Answer: (C) Three