SAT Practice Test 3, Section 2: Questions 11 - 15

This is for SAT in Jan 2016 or before.

The following are worked solutions for the questions in the math sections of the SAT Practice Tests found in the The Official SAT Study Guide Second Edition.

It would be best that you go through the SAT practice test questions in the Study Guide first and then look at the worked solutions for the questions that you might need assistance in. Due to copyright issues, we are not able to reproduce the questions, but we hope that the worked solutions will be helpful.

11. Correct answer: (C)

Given:
The diameter of the front wheel is the diameter of the back wheel

To find:
The number of revolutions the front wheel makes for one revolution of the back wheel

Solution:
Topic(s): Circumference of circle, ratio

C = πd

Circumference is directly proportional to the diameter, so we can use the ratio of the diameters as the ratio of the circumferences

Ratio of back wheel to front wheel is

1 revolution of the back wheel would result in 2 revolutions of the front wheel.

Answer: (C) 2

12. Correct answer: (C)

Given:
A list of numbers with p positive and n negative numbers

The probability that a number picked is positive is

To find:
Value of

Solution:
Topic(s): Probability

Probability that the number is positive is

If we take the number of positive numbers to be 3x then the total numbers in the list would be 5x.

The number of negative numbers would be 5x – 3x = 2x.

Answer: (C)

13. Correct answer: (B)

Given:
The cost of producing x units is
k is a constant

20 units produced at the cost of $640

To find:
The value of k

Solution:
20 units were produced at the cost of $640. Substitute x =20

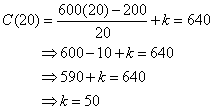
Answer: (B) 50

14. Correct answer: (A)

Given:
2x + 3y < 6

To find:
Ordered pairs of positive integers (x, y)

Solution:
2x + 3y < 6

(x, y) are ordered pairs of positive integers.

Be careful! 0 is not a positive integer.

Consider the ordered pair (1,1)

2 + 3 = 5 < 6

Any other ordered pairs (1,2), (2,1) etc would have a result greater than 6. So, there is only one ordered pair that fits the condition.

Answer: (A) One

15. Correct answer: (C)

Given:
The figures
y = 60

To find:
How much greater is perimeter of triangle ABC than the perimeter of triangle DEF

Solution:
Topic(s): Types of triangles

Triangle ABC has two equal angles.

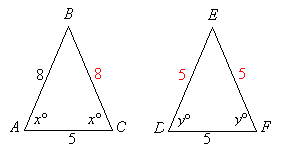
So, BC is 8. (If two angles of a triangle are equal, then the sides opposite those angles are equal)

DE = EF = DF = 5 (If two angles of a triangle are each equal to 60º, then all the sides of the triangle are equal in length)

Perimeter of triangle ABC = 8 + 8 + 5 = 21

Perimeter of triangle DEF = 5 + 5 + 5 = 15

Perimeter of triangle ABC – Perimeter of triangle DEF = 21 – 15 = 6

Answer: (C) 6