Factor Trinomials with Two Variables

Related Pages
Factoring Trinomials
More Algebra Lessons

The following diagram shows how to factor trinomials with two variables. This method only works when the leading coefficient is one. Scroll down the page for examples and solutions for other methods.

 

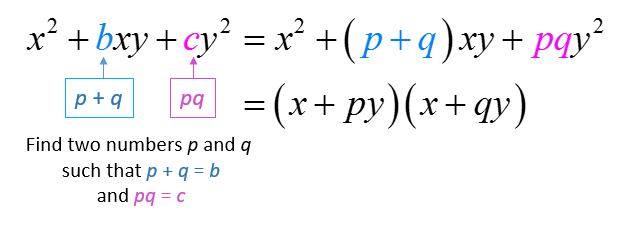
How to factor Trinomials with two variables?
Sometimes a trinomial may consists of two variables. We can factor the trinomial in a similar way as if it has only one variable. We can use the trial and error method (reverse FOIL method), the grouping method or the AC method.

Example:
Factor the following trinomials:
a) e² − 6ef + 9f²
b) 2x² + 7xy − 15y²

Solution:
a) e² − 6ef + 9f² = (e − 3f)²
b) 2x² + 7xy − 15y² = (2x − 3y)(x + 5y)

Factoring trinomials with two variables
Step 1: Find the Product, Sum and the two numbers that “work”
Product = (First number) × (Last number)
Sum = (Middle Number)
Find two numbers that when multiplied gives the Product and when added gives the Sum.
Step 2: Split the middle term.
Step 3: Group in twos and remove the GCF of each group.
Step 4: Write in factored form.

How to factor trinomials with two variables and a = 1?
Some strategies to factor trinomials that have a = 1

Examples:

1. a² - 9ab + 14b²
2. m² - mn - 30n²

• Show Video Lesson

How to factor trinomial with two variables and a > 1?

Example:
18m² - 9mn - 2n²

• Show Video Lesson

Factor trinomial containing two variables
Example:
v² + 5vf - 24f²

• Show Video Lesson

How to factor trinomial with two variables using gcf then grouping?
Example:
6m⁶n + 11m⁵n² + 3m⁴n³

• Show Video Lesson

How to factor a trinomial with two variables using the AC Method?
Example:
30x³y - 25x²y² - 30xy³

• Show Video Lesson

How to Factor Trinomials with Two Variables using the reverse FOIL or trial and error method?
Examples:

1. 12x² - 5xy - 2y²
2. 6x² - 17xy + 10y²

• Show Video Lesson

Example:

1. 2c² + 13cd + 6d²
2. 5x² - 6xy + 1

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.