Solving Equations With Two Variables

Linear Equation In Two Variables

A linear equation in two variables, x and y, can be written in the form
ax + by = c
where x and y are real numbers and a and b are not both zero.

For example, 3x + 2y = 8 is a linear equation in two variables.

A solution of such an equation is an ordered pair of numbers (x, y) that makes the equation true when the values of x and y are substituted into the equation.

For example, both (2, 1) and (0, 4) are solutions of the equation but (2, 0) is not a solution. A linear equation in two variables has infinitely many solutions.

The following video shows how to complete ordered pairs to make a solution to linear equations.

• Show Video Lesson

Systems of Equations or Simultaneous Equations

The following diagram shows examples of how to solve systems of equations using substitution or elimination.. Scroll down the page for more examples and solutions on how to solve systems of equations or simultaneous equations..

If another linear equation in the same variables is given, it is usually possible to find a unique solution of both equations. Two equations with the same variables are called a system of equations, and the equations in the system are called simultaneous equations. To solve a system of two equations means to find an ordered pair of numbers that satisfies both equations in the system.

There are two basic methods for solving systems of linear equations, by substitution or by elimination.

Substitution Method

In the substitution method, one equation is manipulated to express one variable in terms of the other. Then the expression is substituted in the other equation.

For example, to solve the system of equations
3x + 2y = 2
y + 8 = 3x

Isolate the variable y in the equation y + 8 = 3x to get y = 3x – 8.

Then, substitute 3x – 8 for y into the equation 3x + 2y = 2.
3x + 2 (3x – 8) = 2
3x + 6x – 16 = 2
9x – 16 = 2
9x = 18

Substitute x = 2 into y = 3x – 8.to get the value for y
y = 3 (2) – 8
y = 6 – 8 = – 2

Answer: x = 2 and y = –2

How to solve simultaneous equations using substitution?

• Show Video Lesson

Elimination Method

In the elimination method, the object is to make the coefficients of one variable the same in both equations so that one variable can be eliminated either by adding the equations together or by subtracting one from the other.

Consider the following example:
2x + 3y = –2 4x – 3y = 14

In this example the coefficients of y are already opposites (+3 and –3). Just add the two equations to eliminate y.

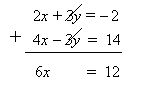
6x = 12

To get the value of y, we need to substitute x = 2 into the equation 2x + 3y = –2
2(2) + 3y = –2
4 + 3y = –2
3y = –6
y = –2

Answer: x = 2 and y = –2

How to solve simultaneous equations using the substitution method and elimination (or combination) method

• Show Video Lesson

Example of the GRE Quantitative Comparison question that involves simultaneous equations

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.