Division using the Area Model

Related Pages
Lesson Plans and Worksheets for Grade 4
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 4
Common Core For Grade 4

Common Core Standards: 4.NBT.6, 4.OA.3

Topic E: Division of Tens and Ones with Successive Remainders

New York State Common Core Math Grade 4, Module 3, Lesson 20
Worksheets for Grade 4

The following figure shows an example of division using the area model. Scroll down the page for more examples and solutions.

 

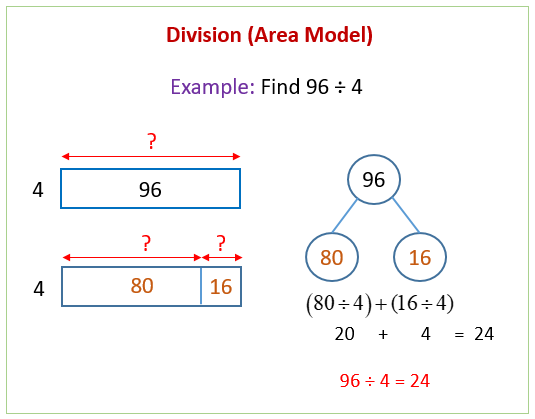
NYS Math Grade 4, Module 3, Lesson 20 Concept Development
Problem 1: Decompose 48 ÷ 4 from whole to part.
Problem 2: Decompose 96 ÷ 4 from whole to part.

• Show Video Lesson

NYS Math Grade 4, Module 3, Lesson 20 Problem Set

1. Alfonso solved a division problem by drawing an area model.
   a. Look at the area model. What division problem did Alfonso solve?
   b. Show a number bond to represent Alfonso’s area model. Start with the total and then show how the total is split into two parts. Below the two parts, represent the total length using the distributive property and then solve.
2. Solve 45 ÷ 3 using an area model. Draw a number bond and use the distributive property to solve for the unknown length.
3. Solve 60 ÷ 4 using an area model. Draw a number bond to show how you partitioned the area, and represent the division with a written method.
4. Solve 72 ÷ 4 using an area model. Explain, using words, pictures, or numbers, the connection of the distributive property to the area model.
5. Solve 72 ÷ 6 using an area model and the standard algorithm.

• Show Video Lesson

NYS Math Module 3 Grade 4 Lesson 20 Homework

1. Maria solved the following division problem by drawing an area model.
   a. Look at the area model. What division problem did Maria solve?
   b. Show a number bond to represent Maria’s area model. Start with the total and then show how the total is split into two parts. Below the two parts, represent the total length using the distributive property and then solve.
2. Solve 42 ÷ 3 using an area model. Draw a number bond and use the distributive property to solve for the unknown length.
3. Solve 60 ÷ 4 using an area model. Draw a number bond to show how you partitioned the area, and represent the division with a written method.
4. Solve 72 ÷ 4 using an area model. Explain, using words, pictures, or numbers, the connection of the distributive property to the area model.
5. Solve 96 ÷ 6 using an area model and the standard algorithm.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.