Cyclic Quadrilaterals and Angles in Semi-Circle
Examples, solutions, videos, worksheets, games and activities to help Geometry students learn about cyclic quadrilaterals and angles in a semi-circles.
Cyclic Quadrilateral
A cyclic quadrilateral has vertices on the same circle and is inscribed in the circle. The opposite angles have the same endpoints (the other vertices) and together their intercepted arcs include the entire circle. Since the measure of an inscribed angle is half the intercepted arc, the sum of the opposite angles must be 180 degrees.
The following diagram shows a cyclic quadrilateral and its properties. Scroll down the page for more examples and solutions.
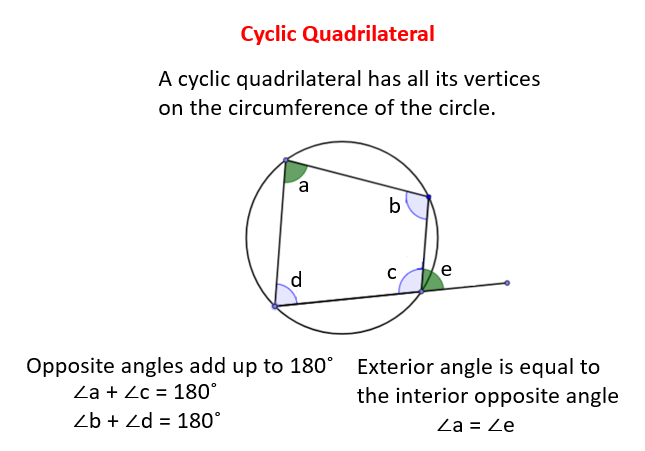
Proof of angles in a Cyclic Quadrilateral
This video explains why the opposite angles in a cyclic quadrilateral add up to 180 degrees.
Angles in Semicircle
If an angle is inscribed in a semicircle, it will be half the measure of a semicircle (180 degrees), therefore measuring 90 degrees. Angles in semicircle is one way of finding missing missing angles and lengths. Pythagorean theorem can be used to find missing lengths (remember that the diameter is the hypotenuse). Also, the measure of an angle formed by a chord to a tangent is half the intercepted arc.
Angles in a semi-circle are 90 degrees This circle theorem can be looked at in two ways, either as ‘angle at the center is twice the angle at circumference’ or ‘angles in a semi-circle are 90 degrees’
A demonstration of the Circle Theorem that the Angle in a Semicircle is a Right Angle.
How to use Angles in a semi-circle theorem to find missing sides and angles?
Circle Properties (cyclic quadrilateral, central and inscribed angle and semi-circles)
How to use circle properties to find missing sides and angles
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.