Conditions For A Unique Triangle

New York State Common Core Math Grade 7, Module 6, Lesson 9

Worksheets for 7th Grade, Module 6, Lesson 9 (pdf)

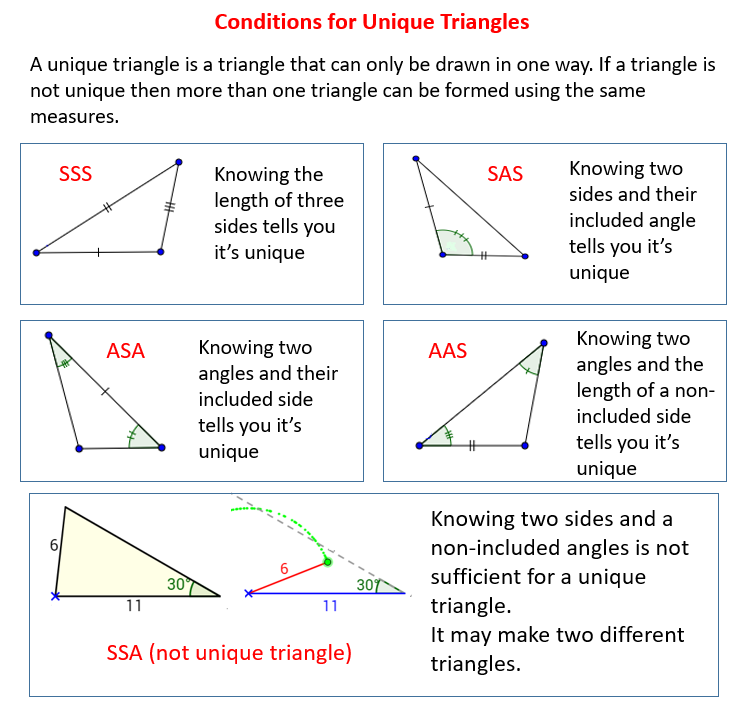
The following figures give the Conditions for a Unique Triangle. Scroll down the page for more examples and solutions.

Triangles-Side Lengths and Unique Triangles

• Show Video Lesson

Lesson 9 Student Outcomes

• Students understand that two triangles are identical if all corresponding sides are equal under some correspondence; three side lengths of a triangle determine a unique triangle.

• Students understand that two triangles are identical if two corresponding sides and the included angle are equal under some correspondence; two sides and an included angle of a triangle determine a unique triangle.

Lesson 9 Summary

• By drawing triangles under the three sides condition and the two sides and an included angle condition, we saw that there is only one way to draw triangles under each of the conditions, which determines a unique triangle.

Lesson 9 Classwork

Opening
Students have learned that triangles are identical if there is a correspondence between the triangles that matches equal sides to angles of equal measurement. What conditions on a triangle always produce identical triangles? In other words, what conditions on a triangle determine a unique triangle?

• Given a triangle, we consider conditions on the triangle such as the measurements of angles, the measurements of sides, and the relationship between those angles and sides.

• If we measure all of the angles and sides and give all the relationships between angles and sides, then any other triangle satisfying the same conditions will be identical to our given triangle.

• If we give too few conditions on a triangle, such as the length of one side and the measurement of one angle, then there will be many non-identical triangles that satisfy the conditions.

• Sometimes just a few specific conditions on a triangle make it so that every triangle satisfying those conditions is identical to the given triangle. In this case, we say the conditions on a triangle determine a unique triangle; that is, all triangles created using those conditions will be identical.

Exploratory Challenge

1. A triangle XYZ exists with side lengths of the segments below. Draw a triangle X’Y’Z’ with the same side lengths as XYZ. Use your compass to determine the sides of X’Y’Z’. Use your ruler to measure side lengths. Leave all construction marks as evidence of your work, and label all side and angle measurements.
   Under what condition is X’Y’Z’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why. Do the results differ from your predictions?

2. ABC is located below. Copy the sides of the triangle to create A’B’C’. Use your compass to determine the sides of A’B’C’. Use your ruler to measure side lengths. Leave all construction marks as evidence of your work, and label all side and angle measurements.
   Under what condition is A’B’C’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.

3. A triangle DEF has an angle of 40° adjacent to side lengths of 4 cm and 7 cm. Construct D’E’F’ with side lengths D’E’ = 4 cm, D’F’ = 7 cm, and included angle ∠D = 40°. Use your compass to draw the sides of D’E’F’. Use your ruler to measure side lengths. Leave all construction marks as evidence of your work, and label all side and angle measurements.
   Under what condition is D’E’F’ drawn? Compare the triangle you drew to two of your peers’ triangles. Did the condition determine a unique triangle? Use your construction to explain why.

4. XYZ has side lengths XY = 2.5 cm, XZ = 4 cm, and ∧X = 120°. Draw X’Y’Z’ under the same conditions. Use your compass and protractor to draw the sides of X’Y’Z’. Use your ruler to measure side lengths. Leave all construction marks as evidence of your work, and label all side and angle measurements.
   Under what condition is X’Y’Z’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.