Probability: Complementary Events

Related Pages
Probability Of An Event
Independent Events
Dependent Events
Mutually Exclusive Events
More Lessons on Probability

The following diagram explains Complementary Events. Scroll down the page for examples and solutions.

 

Printable & Online Probability Worksheets

If the probability of an event, A, is P(A), then the probability that the event would not occur (also called the complementary event) is 1 – P(A).

Example:
.

What is the probability of not getting a white ball?

Solution:


 

Example:
.

What is the probability of drawing a blue card?

Solution:
Let A = event of drawing a red card

B = event of drawing a blue card

P(B) is the probability of drawing a blue card which is also the same as the probability of not drawing a red card (Since the cards are either red or blue)

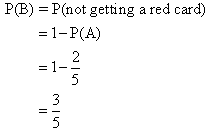
A and B are called complementary events. This may be denoted as:

P(A ’ ) = P(B) (recall in sets that A ’ is the complement of A)

P(A) = P(B ’ )

We can generally state that: P(A) + P(A ’ ) = 1

Example:
A number is chosen at random from a set of whole numbers from 1 to 50. Calculate the probability that the chosen number is not a perfect square.

Solution:
Let A be the event of choosing a perfect square.

Let A’ be the event that the number chosen is not a perfect square.

A = {1, 4, 9, 16, 25, 36, 49}

Number of elements in A, n(A) = 7

Total number of elements, n(S) = 50

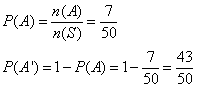
The probability that the number chosen is not a perfect square is

The Probability of Complementary Events

1. A standard deck of cards has 52 cards.
   a) What is the probability of drawing an ace from the shuffled deck of cards?
   b) What is the probability of drawing anything but an ace?

2. A bag contains 12 identically shaped blocks, 3 of which are red and the remainder are green. The bag is well shaken and a single block is drawn.
   a) What is the probability that the block is red?
   b) What is the probability that the block is not red?

• Show Video Lesson

Example of calculating the probability of complementary events

• Show Video Lesson

Probability of the Complement of an Event

Examples:

1. An airline reports that 94% of its flights arrive on time. What is the probability that a flight will be late?

2. In a bag containing 29 marbles, 5 of the marbles are red and 2 are green. What is the probability of randomly selecting a marble that is neither red nor green?

• Show Video Lesson

Probability of Complementary Events and “At Least One” Probabilities
“At least one” is equivalent to “one or more”
The complement of getting at least one item of a particular type is that you get no items of that type.

Examples:

1. Find the probability of couple having at least 1 boy among 4 children.
2. A unprepared student makes random guesses for the ten true-false questions on a quiz. Find the probability that there is at least one correct answer.
3. Find the probability of selecting at least one blue marble from a bag of 5 blue and 4 green when 3 marbles are selected.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.