Circle Theorem Examples
In this lesson, we will learn
- a Circle Theorem called the Thales' Theorem or Triangle inscribed in semicircle or Angle inscribed in semicircle or “90 degrees in Semicircle” Theorem.
- how to use the Thales' Theorem to find missing angles.
- how to prove the Thales' Theorem.
Thales' theorem
The Thales' theorem states
Every angle subtended at the circumference by the diameter of a circle is a right angle (90˚).
or
The diameter of a circle always subtends a right angle to any point on the circle.
or
The angle inscribed in a semicircle is 90˚.
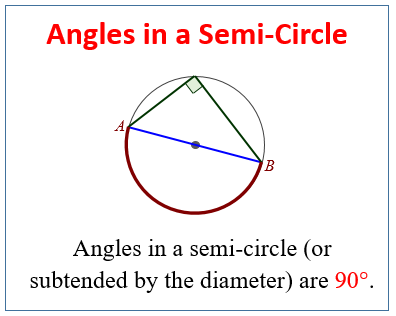
The following diagram shows the Thales' Theorem: Angles in a semi-circle are 90°. Scroll down the page for more examples and solutions.
Using the Theorem
Example:
O is the centre of the circle. Find the value of x

Solution:
∠ABC = 90˚ ( angle in a semicircle = 90˚)
63˚ + 90˚ + x = 180˚ ( sum of angles in a triangle )
x = 27˚
Inscribed Right Triangles (Right Triangles Inside of Circles)
Thales' Theorem: If the longest side of a triangle inscribed within a circle is the same length as the diameter of a circle, then that triangle is a right triangle, as well as the converse: if a right triangle is inscribed within a circle, the length of its hypotenuse is the diameter of the circle.
We can use the Thales' Theorem to find missing angles.
Proving the Theorem
Proof of the Thales' Theorem
Proof showing that a triangle inscribed in a circle having a diameter as one side is a right triangle.
This proof uses the bow theorem.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.